
科目:gzsx 来源:天骄之路中学系列 读想用 高二数学(上) 题型:013
方程![]() =1所表示曲线为C,甲:若曲线C为椭圆,则1<t<4;乙:若曲线C为双曲线,则t>4或t<1;丙:曲线C不可能是圆;丁:若曲线C表示椭圆且长轴在x轴上,则1<t<
=1所表示曲线为C,甲:若曲线C为椭圆,则1<t<4;乙:若曲线C为双曲线,则t>4或t<1;丙:曲线C不可能是圆;丁:若曲线C表示椭圆且长轴在x轴上,则1<t<![]() ,以上命题正确的有
,以上命题正确的有
A.2个
B.3个
C.1个
D.4个
科目:gzsx 来源: 题型:
设![]() ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量![]() ,向量
,向量![]() ,
,![]() ,动点
,动点![]() 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状; w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)已知![]() ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且![]() (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知![]() ,设直线
,设直线![]() 与圆C:
与圆C:![]() (1<R<2)相切于A1,且
(1<R<2)相切于A1,且![]() 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
科目:gzsx 来源: 题型:
设![]() ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量![]() ,向量
,向量![]() ,
,![]() ,动点
,动点![]() 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状; ![]()
![]()
(2)已知![]() ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且![]() (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知![]() ,设直线
,设直线![]() 与圆C:
与圆C:![]() (1<R<2)相切于A1,且
(1<R<2)相切于A1,且![]() 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
科目:gzsx 来源:2014届四川省高二4月数学试卷(解析版) 题型:解答题
设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知 ,设直线
,设直线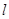 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且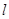 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
科目:gzsx 来源: 题型:解答题
设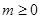 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量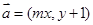 ,向量
,向量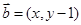 ,
,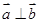 ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知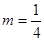 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且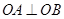 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知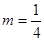 ,设直线
,设直线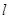 与圆C:
与圆C: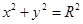 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且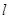 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
科目:gzsx 来源:2010届高三数学每周精析精练:直线和圆 题型:解答题
设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量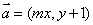 ,向量
,向量 ,
,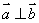 ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知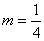 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知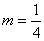 ,设直线
,设直线 与圆C:
与圆C: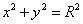 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
科目:gzsx 来源:不详 题型:解答题
 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E. ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程; ,设直线
,设直线 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.科目:gzsx 来源: 题型:013
方程 所表示的曲线是
所表示的曲线是
[
]A
.以(2,4)为顶点的抛物线 B.以(-4,-2)为顶点的抛物线C
.以(4,10)为顶点的抛物线 D.以(-4,10)为顶点的抛物线科目:gzsx 来源:2012届山西大学附中高二年级五月月考数学试题(理科) 题型:选择题
方程 所表示的曲线为
所表示的曲线为
A.焦点在 轴上的椭圆 B.焦点在
轴上的椭圆 B.焦点在 轴上的椭圆
轴上的椭圆
C.焦点在 轴上的双曲线 D.焦点在
轴上的双曲线 D.焦点在 轴上的双曲线
轴上的双曲线
科目:gzsx 来源:2012届山西大学附中高二年级五月月考数学试题(文科) 题型:选择题
方程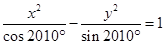 所表示的曲线为
所表示的曲线为
A.焦点在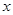 轴上的椭圆 B.焦点在
轴上的椭圆 B.焦点在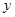 轴上的椭圆
轴上的椭圆
C.焦点在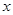 轴上的双曲线 D.焦点在
轴上的双曲线 D.焦点在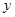 轴上的双曲线
轴上的双曲线
科目:gzsx 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
方程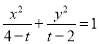 所表示的曲线为C,有下列命题:
所表示的曲线为C,有下列命题:
①若曲线C为椭圆,则 ;
;
②若曲线C为双曲线,则 或
或 ;
;
③曲线C不可能为圆;
④若曲线C表示焦点在 上的双曲线,则
上的双曲线,则 。
。
以上命题正确的是 。(填上所有正确命题的序号)
科目:gzsx 来源: 题型:填空题
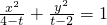 所表示的曲线为C,有下列命题:
所表示的曲线为C,有下列命题:科目:gzsx 来源:2011-2012学年山西省运城市临猗中学高二(上)周考数学试卷(4)(理科)(解析版) 题型:填空题
 所表示的曲线为C,有下列命题:
所表示的曲线为C,有下列命题:科目:gzsx 来源:2010-2011学年陕西省西安市八校高三联考数学试卷3(文科)(解析版) 题型:选择题
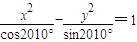 所表示的曲线为( )
所表示的曲线为( )