科目:czsx 来源: 题型:
| 1 | 2 |
科目:czsx 来源: 题型:解答题
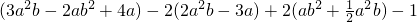 的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.
的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.科目:czsx 来源:不详 题型:解答题
| 1 |
| 2 |
科目:czsx 来源:四川省期末题 题型:解答题
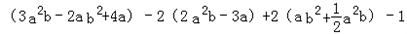 的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.
的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.科目:czsx 来源: 题型:
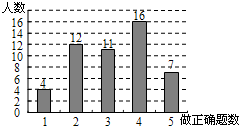
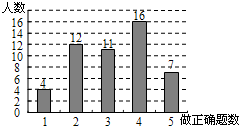 在学习解二元一次方程组时,数学老师布置了5道解方程组的课堂练习题,下课时统计全班同学解答正确的题数,情况绘成了下面的条形统计图.请你根据统计图提供的信息,计算每个学生做对的平均题数是
在学习解二元一次方程组时,数学老师布置了5道解方程组的课堂练习题,下课时统计全班同学解答正确的题数,情况绘成了下面的条形统计图.请你根据统计图提供的信息,计算每个学生做对的平均题数是科目:czsx 来源: 题型:填空题
 在学习解二元一次方程组时,数学老师布置了5道解方程组的课堂练习题,下课时统计全班同学解答正确的题数,情况绘成了下面的条形统计图.请你根据统计图提供的信息,计算每个学生做对的平均题数是________.
在学习解二元一次方程组时,数学老师布置了5道解方程组的课堂练习题,下课时统计全班同学解答正确的题数,情况绘成了下面的条形统计图.请你根据统计图提供的信息,计算每个学生做对的平均题数是________.科目:czsx 来源:不详 题型:填空题
科目:czsx 来源: 题型:


科目:czsx 来源:2014-2015学年山西省阳泉市平定县九年级下学期中考一模数学试卷(解析版) 题型:解答题
【问题情境】一节数学课后,老师布置了一道课后练习题:
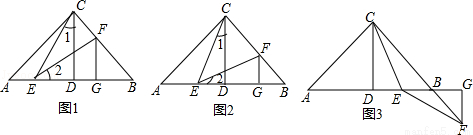
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写这道练习题的证明过程;

(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
科目:czsx 来源:2016届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.

(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
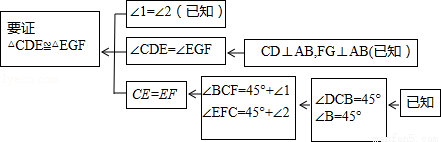
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
科目:czsx 来源:2016届黑龙江大庆五十一中九年级下期中考试数学试卷(解析版) 题型:解答题
【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示:
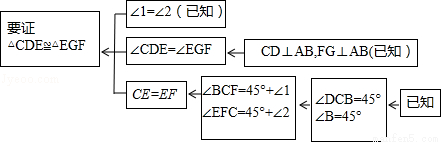
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
科目:czyw 来源:非常讲解·教材全解全析 语文 九年级上 配人教课标 人教课标 题型:056
写作
对本课练习题四进行扩展。如果菲利普夫妇在船上发现于勒真的成了大富豪,他们将会怎样做?试以“叔叔荣归故里”为题写一篇短篇小说。
科目:czsx 来源:2013年初中毕业升学考试(浙江湖州卷)数学(带解析) 题型:解答题
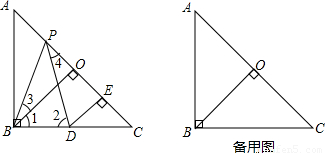
一节数学课后,老师布置了一道课后练习题:
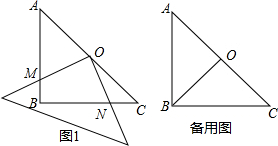
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.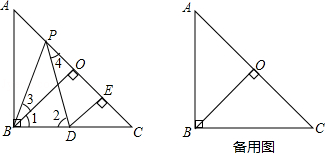
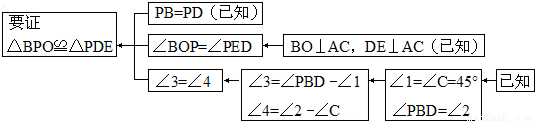
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示: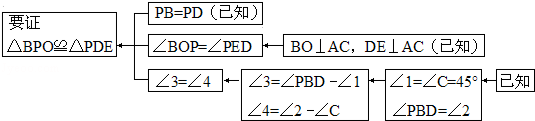
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
科目:czsx 来源:2013年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:解答题
一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
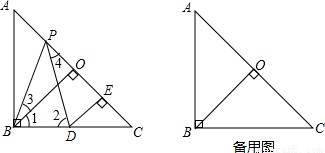
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
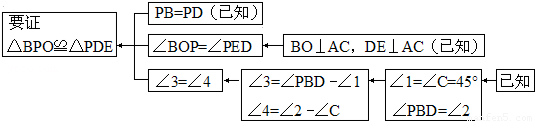
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
科目:czsx 来源: 题型:解答题

科目:czsx 来源: 题型:
一节数学课后,老师布置了一道课后练习题:
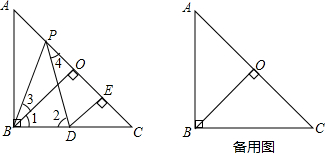
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
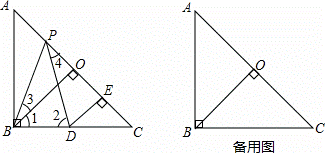
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
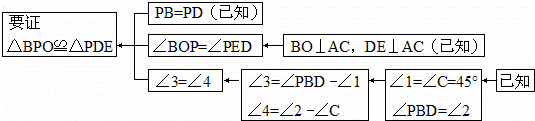
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
科目:czsx 来源:2013年浙江省湖州市中考数学试卷(解析版) 题型:解答题