
科目:czsx 来源: 题型:阅读理解
| 1-x |
| x-1 |
| 1-x |
| x-1 |
| 1-2x |
| 2x-1 |
科目:czsx 来源: 题型:
| 2ax |
| 3 |
| 3 |
| 2 |
| 15 |
| 4a |
科目:czsx 来源: 题型:解答题
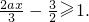
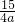 ③
③科目:czsx 来源: 题型:阅读理解
| ||
| 50个101 |
| ||
| 100个101 |
科目:czsx 来源: 题型:阅读理解
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
科目:czsx 来源:2003年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
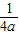 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0, )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;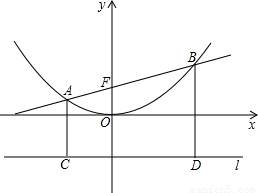
科目:czsx 来源: 题型:解答题
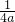 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0,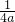 )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;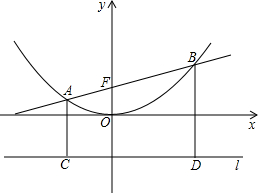
科目:czsx 来源:2003年湖北省黄石市中考数学试卷(解析版) 题型:解答题
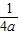 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0,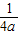 )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;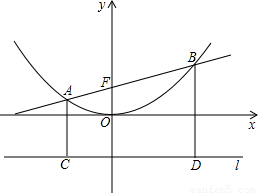
科目:czsx 来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版 题型:044
先阅读下面一段材料,再完成后面的问题:
材料 过抛物线y=ax2(a>0)的对称轴上一点(0,-![]() ),作对称轴的垂线l,则抛物线上任意一点P到点F(0,
),作对称轴的垂线l,则抛物线上任意一点P到点F(0,![]() )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,![]() ).
).
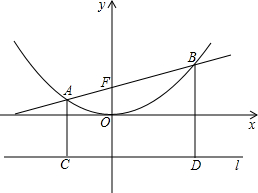
问题 若直线y=kx+b交抛物线y=![]() x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
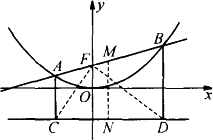
(1)求抛物线y=![]() x2的焦点F的坐标;
x2的焦点F的坐标;
(2)求证:直线AB过焦点时,CF⊥DF;
(3)当直线AB过点(-1,0),且以线段AB为直径的圆与准线l相切时,求这条直线对应的函数解析式.
科目:czsx 来源:不详 题型:解答题
| ||
| 50个101 |
| ||
| 100个101 |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:阅读理解
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 5 |
科目:czsx 来源: 题型:阅读理解
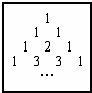 27、阅读下面一段材料,回答问题.
27、阅读下面一段材料,回答问题.科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
| a-2 |
| a2-4 |
| 2 |
| 2-a |
| a-3 |
| (a+2)(a-2) |
| 2 |
| a-2 |
| a-3 |
| (a+2)(a-2) |
| 2(a+2) |
| (a+2)(a-2) |
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
|
|
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 5x+1 |
| 2x-3 |
科目:czsx 来源:期中题 题型:解答题
科目:czsx 来源:同步题 题型:解答题
先阅读下面例题的解题过程,再解答后面的问题:
例:已知代数式9-6y-4y2=7,求2y2+3y+7的值,
解:由9-6y-4y2=7,得-6y-4y2=7-9,即6y+4y2=2,
因此2y2+3y=1,所以2y2+3y+7=8,
问题:已知代数式14x +5-21x2的值是-2,求 6x2-4x+5的值。