精英家教网 >
试题搜索列表 >若△ABC相似△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2
若△ABC相似△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2答案解析
科目:czsx
来源:
题型:
106、若△ABC∽△DEF,△ABC的面积为81cm
2,△DEF的面积为36cm
2,且AB=12cm,则DE=
8
cm.
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE=______cm.
查看答案和解析>>
科目:czsx
来源:《第29章 相似形》2010年整章水平测试(解析版)
题型:填空题
若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE= cm.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE=________cm.
查看答案和解析>>
科目:czsx
来源:同步题
题型:填空题
若△ABC∽△DEF,△ABC的面积为81cm2,△DEF的面积为36cm2,且AB=12cm,则DE= _________ cm.
查看答案和解析>>
科目:czsx
来源:
题型:
已知△ABC∽△DEF,相似比为2:1,若△DEF的面积为4,则△ABC的面积为
16
16
.
查看答案和解析>>
科目:czsx
来源:
题型:
若△ABC∽△DEF,相似比为1:2,且△ABC的面积为4,则△DEF的面积为( )
查看答案和解析>>
科目:czsx
来源:
题型:
若△ABC∽△DEF,相似比为2,且△ABC的面积为12,则△DEF的面积为( )
查看答案和解析>>
科目:czsx
来源:2012届北京市丰台区九年级上学期期末考试数学卷
题型:选择题
若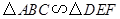 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
A.16
B.8 C.4
D.2
查看答案和解析>>
科目:czsx
来源:不详
题型:单选题
若△ABC
∽△DEF,相似比为2,且△ABC的面积为12,则△DEF的面积为( )
查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市丰台区九年级(上)期末数学试卷(解析版)
题型:选择题
若△ABC∽△DEF,相似比为1:2,且△ABC的面积为4,则△DEF的面积为( )
A.16
B.8
C.4
D.2
查看答案和解析>>
科目:czsx
来源:2010-2011学年安徽省安庆市九年级(上)期中数学试卷(解析版)
题型:选择题
若△ABC∽△DEF,相似比为2,且△ABC的面积为12,则△DEF的面积为( )
A.3
B.6
C.24
D.48
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
已知△ABC∽△DEF,相似比为2:1,若△DEF的面积为4,则△ABC的面积为______.
查看答案和解析>>
科目:czsx
来源:
题型:
若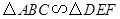 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
A.16 B.8 C.4 D.2
查看答案和解析>>
科目:czsx
来源:2011-2012学年北京市丰台区九年级上学期期末考试数学卷
题型:单选题
若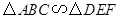 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
查看答案和解析>>
科目:czsx
来源:
题型:
若
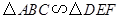
,相似比为1∶2,且△
ABC的面积为4,则△
DEF的面积为
查看答案和解析>>
科目:czsx
来源:
题型:填空题
已知△ABC∽△DEF,相似比为2:1,若△DEF的面积为4,则△ABC的面积为________.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
若△ABC∽△DEF,相似比为1:2,且△ABC的面积为4,则△DEF的面积为
- A.
16
- B.
8
- C.
4
- D.
2
查看答案和解析>>
科目:czsx
来源:
题型:单选题
若△ABC∽△DEF,相似比为2,且△ABC的面积为12,则△DEF的面积为
- A.
3
- B.
6
- C.
24
- D.
48
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读与理解:
三角形的中线的性质:三角形的中线等分三角形的面积,
即如图1,AD是△ABC中BC边上的中线,
则
S△ABD=S△ACD=S△ABC.
理由:∵BD=CD,∴
S△ABD=BD×AH=CD×AH=S△ACD=
S△ABC,
即:等底同高的三角形面积相等.
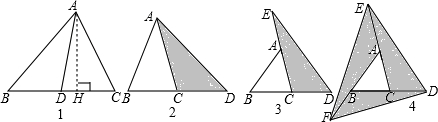
操作与探索
在如图2至图4中,△ABC的面积为a.
(1)如图2,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S
1,则S
1=
(用含a的代数式表示);
(2)如图3,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S
2,则S
2=
(用含a的代数式表示),并写出理由;
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图4).若阴影部分的面积为S
3,则S
3=
(用含a的代数式表示).
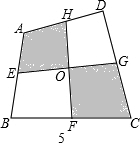
拓展与应用
如图5,已知四边形ABCD的面积是a,E、F、G、H分别是AB、BC、CD的中点,求图中阴影部分的面积?
查看答案和解析>>

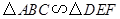 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为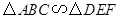 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
