如图，点E在AB上，点D在AC上，且∠B＝∠C答案解析

科目：czsx 来源：非常讲解·教材全解全析　数学　九年级下　（配北师大课标） 配北师大课标 题型：047

如图，⊙O的弦AB、CD的延长线交于P，且PA＝PC．O到弦AB,CD的距离相等。

求证：PB＝PD．

科目：czsx 来源： 题型：

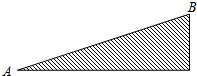甲、乙二人在如图所示的斜坡AB上作往返跑训练．已知：甲上山的速度是a米/分，下山的速度是b米/分（a＜b）；乙上山的速度是

1

2

a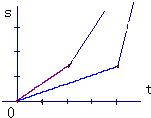米/分，下山的速度是2b米/分．如果甲、乙二人同时从点A出发，时间为t（分），离开点A的路程为S（米）．那么下面图象中，大致表示甲、乙二人从点A出发后的时间t（分）与离开点A的路程S（米）之间的函数关系的是（　　）

A、

B、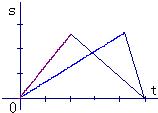

C、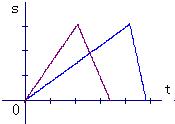

D、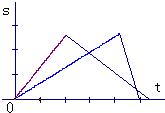

科目：czsx 来源： 题型：

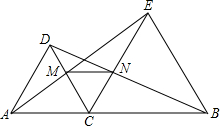（2013•明溪县质检）如图，C是线段AB上一动点，分别以AC、BC为边作等边△ACD．等边△BCE，连接AE、BD分别交CD、CE于M、N两．
（1）求证：AE=BD；
（2）判断直线MN与AB的位置关系；
（3）若AB=10，当点C在AB上运动时，是否存在一个位置使MN的长最大？若存在请求出此时AC的长以及MN的长．若不存在请说明理由．

科目：czsx 来源： 题型：

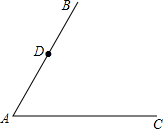如图，D是射线AB上一点，过点D作DE∥AC，交∠BAC平分线于E，过点D作DF⊥AE，垂足为F．
（1）按要求在右图上将图形补全；
（2）已知∠BAC=60°，AD=2，求线段EF的长．

科目：czsx 来源： 题型：

如图，△ABC中，AB=20，BC=21，AC=13，如果动点D以每秒2个单位长的速度从点B出发沿射线BA方向运动，当运动到12秒时停止，直线DE∥BC，E为直线DE与直线CA的交点，若点D运动时间设为t秒．
（1）求当点D在线段AB上时线段DE的长度（用含t的代表式表示）；
（2）求出△DEC的面积S与时间t的函数关系式；
（3）S是否有最大值？若有，请求出最大值和相应t的值；若没有，请说明理由．

科目：czsx 来源： 题型：

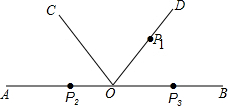
如图，O是直线AB上任意一点，OC平分∠AOB．按下列要求画图并回答问题：
（1）分别在射线OA、OC上截取线段OD、OE，且OE=2OD；
（2）连接DE；
（3）以O为顶点，画∠DOF=∠EDO，射线OF交DE于点F；
（4）写出图中∠EOF的所有余角：

∠DOF，∠EDO

∠DOF，∠EDO

．

科目：czsx 来源： 题型：

10、如图，C为⊙O直径AB上一动点，过点C的直线交⊙O于D，E两点，且∠ACD=45°，DF⊥AB于点F，EG⊥AB于点G，当点C在AB上运动时，设AF=x，DE=y，下列中图象中，能表示y与x的函数关系式的图象大致是（　　）

A、

B、

C、

D、

科目：czsx 来源： 题型：

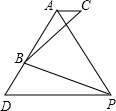已知：如图，△ABC中，AB=3，∠BAC=120°，AC=1，D为AB延长线上一点，BD=1，点P在∠BAC的平分线上，且满足△PAD是等边三角形．
（1）求证：BC=BP；
（2）求点C到BP的距离．

科目：czsx 来源： 题型：

如图，△ABC中，AB=2，BC=2

3

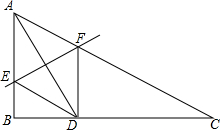，AC=4，E，F分别在AB，AC上，沿EF对折，使点A落在BC上的点D处，且FD⊥BC．
（1）求AD的长；
（2）判断四边形AEDF的形状，并证明你的结论．

科目：czsx 来源： 题型：

（2011•裕华区二模）如图①，将两个等腰直角三角形叠放在一起，使上面三角板的一个锐角顶点与下面三角板的直角顶点重合，并将上面的三角板绕着这个顶点逆时针旋转，在旋转过程中，当下面三角板的斜边被分成三条线段时，我们来研究这三条线段之间的关系．
（1）实验与操作：
如图②，如果上面三角板的一条直角边旋转到CM的位置时，它的斜边恰好旋转到CN的位置，请在网格中分别画出以AM、MN和NB为边长的正方形，观察这三个正方形的面积之间的关系；
（2）猜想与探究：
如图③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB边上的点，∠MCN=45°，作DA⊥AB于点A，截取DA=NB，并连接DC、DM．
我们来证明线段CD与线段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于点A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．

请你继续解答：
①线段MD与线段MN相等吗？为什么？
②线段AM、MN、NB有怎样的数量关系，为什么？
（3）拓广与运用：
如图④，已知线段AB上任意一点M（AM＜MB），是否总能在线段MB上找到一点N，使得分别以AM与BN为边长的正方形的面积的和等于以MN为边长的正方形的面积？若能，请在图④中画出点N的位置，并简要说明作法；若不能，请说明理由．

科目：czsx 来源： 题型：阅读理解

阅读材料解答问题：如图，在菱形ABCD中，AB=AC，过点C作一条直线，分别交AB，AD的延长线于M，N，则

1

AM

+

1

AN

=

1

AC

（1）试证明：

1

AM

+

1

AN

=

1

AC

；

（2）如图，0为直线AB上一点，0C，OD将平角AOB三等分，点P₁，P₂，P₃分别在射线OA，OD，OB上，0P₁=r₁，0P₂=r₂，OP₃=r₃，r与r′分别满足

1

r

=

1

r1

+

1

r2

，

1

r

=

1

r1

+

1

r2

+

1

r3

，用直尺在图中分别作出长度r，r′的线段．

科目：czsx 来源： 题型：

如图，已知直线AB交两坐标于A、B两点，且OA=OB=1，点P（a、b）是双曲线y=

1

2x

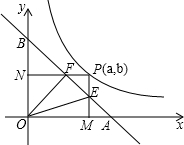上在第一象内的点过点P作PM⊥x轴于M、PN⊥y轴于N．两垂线与直线AB交于E、F．
（1）分别写出点E、F的坐标（分别用a或b表示）；
（2）求△OEF的面积（结果用a、b表示）；
（3）△AOF与△BOE是否相似？请说明理由；
（4）当P在双曲线y=

1

2x

上移动时，△OEF随之变动，观察变化过程，△OEF三内角中有无大小始终保持不变的内角？若有，请指出它的大小，并说明理由．

科目：czsx 来源： 题型：

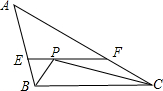如图，△ABC中，AB=4，BC=6cm，AC=8cm，∠B与∠C的角平分线交于点P，EF经过点P，且EF∥BC，点E在AB上，点F在AC上，则EF=

 

cm．

科目：czsx 来源： 题型：

如图，D是射线AB上一点，过点D作DE∥AC，交∠BAC平分线于点E，过点D作DF⊥AE，垂足为F，DF交AC于点G．
（1）按要求在所给图中将图形补全，然后判断四边形ADEG的形状，并证明你的结论；
（2）标出有向线段

AD

、

AF

、

AG

，记向量

AD

=

a

、

AF

=

b

，试用

a

，

b

表示向量

AG

．

科目：czsx 来源： 题型：

（2012•顺义区二模）已知：如图，D为线段AB上一点（不与点A、B重合），CD⊥AB，且CD=AB，AE⊥AB，BF⊥AB，且AE=BD，BF=AD．
（1）如图1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；
（2）如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；
（3）若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．

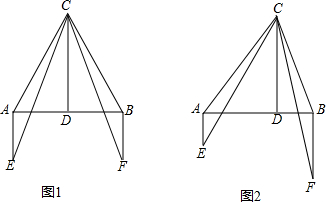
科目：czsx 来源： 题型：

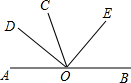如图，O是直线AB上的点，OD是∠AOC的平分线，OE是∠COB的平分线，求∠DOE的度数．
（1）一变：如图，∠DOE=90°，OD平分∠AOC，问OE是否平分∠BOC？
（2）二变：如图，点O在直线AB上，且∠AOC≠∠BOC，OD平分∠AOC，∠DOE=90°，下面四个结论，错误的有（　　）
①图中必有3个钝角；②图中只有3对既相邻又互补的角；③图中没有45°的角；④OE是∠BOC的平分线．
A．0个；B．1个；C．2个；D．3个．

科目：czsx 来源： 题型：

已知：如图，在梯形ABCD中，AD∥BC，BC=3AD．
（1）如图①，连接AC，如果三角形ADC的面积为6，求梯形ABCD的面积；
（2）如图②，E是腰AB上一点，连接CE，设△BCE和四边形AECD的面积分别为S₁和S₂，且2S₁=3S₂，求

AE

BE

的值；
（3）如图③，AB=CD，如果CE⊥AB于点E，且BE=3AE，求∠B的度数．

科目：czsx 来源： 题型：

如图，M是线段AB上一点，且AB=10cm，C，D两点分别从M，B同时出发时1cm/s，3cm/s的速度沿直线BA向左运动，运动方向如箭头所示（C在线段AM上，D在线段BM上）．
（1）当点C，D运动了2s，求这时AC+MD的值．
（2）若点C，D运动时，总有MD=3AC，求AM的长．

科目：czsx 来源： 题型：

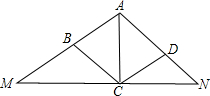
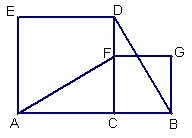23、如图，C是线段AB上一点，分别以AC、BC为边在线段AB同侧作正方形ACDE和BCFG，连接AF、BD．
（1）AF与BD是否相等，为什么？
（2）如果点C在线段AB的延长线上，（1）中的结论是否成立？请作图，并说明理由．

科目：czsx 来源： 题型：

如图，△ABC中，AB=3，BC=4，AC=5，E，F分别在AB，AC上，沿EF对折，使点A落在BC上的点D处，且FD⊥BC．
（1）判断四边形AEDF的形状，并证明你的结论．
（2）求AD的长．