在(-2)三次方,-(-2)三次方,-负2的3次方的绝对值,最大的是答案解析
科目:czsx
来源:
题型:
在数-2.3,-5,0,1中,属于负分数的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•丽水)在数0,2,-3,-1.2中,属于负整数的是( )
查看答案和解析>>
科目:czsx
来源:丽水
题型:单选题
在数0,2,-3,-1.2中,属于负整数的是( )
查看答案和解析>>
科目:czsx
来源:2013年浙江省丽水市中考数学试卷(解析版)
题型:选择题
在数0,2,-3,-1.2中,属于负整数的是( )
A.0
B.2
C.-3
D.-1.2
查看答案和解析>>
科目:czsx
来源:
题型:013
三个有理数相乘的积小于0,则这三个数中负因数的个数是
[ ]
查看答案和解析>>
科目:czsx
来源:
题型:单选题
在数0,2,-3,-1.2中,属于负整数的是
- A.
0
- B.
2
- C.
-3
- D.
-1.2
查看答案和解析>>
科目:czsx
来源:
题型:单选题
三个有理数相乘的积小于0,则这三个数中负因数的个数是
- A.
1个
- B.
2个
- C.
3个
- D.
1个或3个
查看答案和解析>>
科目:czsx
来源:
题型:
在数0,2,-3,-1.2中,属于负整数的是
A. 0 B. 2 C. -3 D. -1.2
查看答案和解析>>
科目:czsx
来源:
题型:
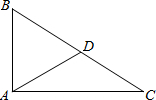
小明、小强、小刚家在如图所示的点A、B、C三个地方,它们的连线恰好构成一个直角三角形,B,C之间的距离为5km,新华书店恰好位于斜边BC的中点D,则新华书店D与小明家A的距离是( )
查看答案和解析>>
科目:czsx
来源:
题型:
某校在一次广播操比赛中,801班,802班,803班的各项得分如下:
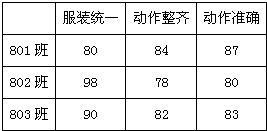
(1)如果根据三项得分的平均数从高到低确定名次,那么三个班的排名顺序怎样?
(2)如果学校认为这三项的重要程度有所不同,而给予这三个项目的权的比为15:35:50.以加权平均数来确定名次,那么三个班的排名又怎样?
查看答案和解析>>
科目:czsx
来源:
题型:
在△ABC中,若∠C=90°,则它的三边满足关系式a
2+b
2=c
2.在此关系式中,涉及到三个量,利用方程的思想,可“知二求一”.
(1)若a=3,b=4,则c=
;
(2)若c=10,b=6,则a=
;
(3)若a:b=3:4,c=20,则a=
,b=
.
查看答案和解析>>
科目:czsx
来源:
题型:
在李咏主持的“幸运52”栏目中,曾有一种竞猜游戏,游戏规则是:在18个商标牌中,有5个商标牌的背面注明了一定的奖金,其余商标牌的背面是一张“哭脸”,若翻到“哭脸”就不获奖.参与这个游戏的观众有三次翻牌的机会,且翻过的牌不能再翻.有一位观众已翻牌两次,一次获奖,一次不获奖,那么这位观众第三次翻牌获奖的概率是
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,B、C、E三点在一条直线上,△ABC和△DCE都为等边三角形,连接AE、DB.

(1)试说出AE=BD的理由.
(2)如果把△DCE绕C点顺时针旋转一个角度,使B、C、E不在一条直线上,(1)中的结论还成立吗?(只回答,不说理由)
(3)在(2)中若AE、BD相交于P,求∠APB的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
下列说法不正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:

已知在锐角△ABC中,I是△ABC三条角平分线的交点,IG⊥BC于G,试比较∠1与∠2的大小,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在一个三位数的百位数字与十位数字之间插入0,1,2,…,9中的一个数码得到的四位数恰是原三位数的9倍,求这样的三位数中最小的数与最大的数分别是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
反比例函数y=
的图象在第一,三象限,则m的取值范围是
;在每一象限内y随x的增大而
.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料并解答问题:
我国是最早了解和应用勾股定理的国家之一,古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用,古希腊数学家毕达哥拉斯首先证明了勾股定理,在西方,勾股定理又称为“毕达哥拉斯定理”.
关于勾股定理的研究还有一个很重要的内容是勾股数组,在《几何》课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b=
(m
2-1)和c=
(m
2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m
2-n
2,b=2mn,c=m
2+n
2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)请根据方法1和方法2按规律填写下列表格:
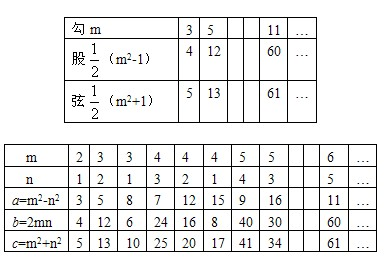
(3)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树
棵.
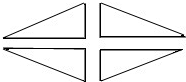
查看答案和解析>>
科目:czsx
来源:
题型:
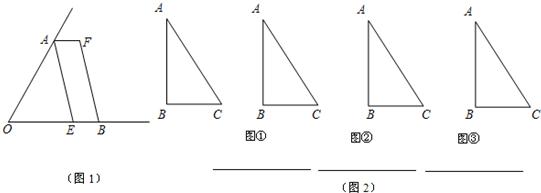
23、(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不要求写作法)
(2)如图2,Rt△ABC中,∠C=90°,AC=4,BC=3,以△ABC的一边为边画等腰三角形,使它的第三个顶点在△ABC的其它边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图下方的横线上写明所画等腰三角形的腰和腰长(不要求尺规作图).
查看答案和解析>>
科目:czsx
来源:
题型:
18、平面上有5个点,其中任意三点都不在同一条直线上,则这些点共可组成
10
个不同的三角形.
查看答案和解析>>

 小明、小强、小刚家在如图所示的点A、B、C三个地方,它们的连线恰好构成一个直角三角形,B,C之间的距离为5km,新华书店恰好位于斜边BC的中点D,则新华书店D与小明家A的距离是( )
小明、小强、小刚家在如图所示的点A、B、C三个地方,它们的连线恰好构成一个直角三角形,B,C之间的距离为5km,新华书店恰好位于斜边BC的中点D,则新华书店D与小明家A的距离是( )



