
科目:czsx 来源:2013届江苏省高邮市九年级下学期适应训练(二模)数学试卷(带解析) 题型:单选题
已知:a+b=m,ab=-4, 化简(a-2)(b-2)的结果是
| A.-2 m | B.2 m | C.2 m-8 | D.6 |
科目:czsx 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:解答题
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.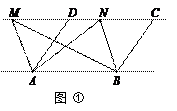
求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由. 
(2)结论应用:
如图③,抛物线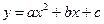 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线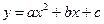 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚ 
科目:czsx 来源: 题型:
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
科目:czsx 来源:2012年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b的大小关系为【 】
A.a>b B.a<b C.a=b D.不能确定
科目:czsx 来源: 题型:
如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC![]() =6,NC=
=6,NC=![]() ,则四边形MABN的面积是
,则四边形MABN的面积是
A.![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()


科目:czsx 来源: 题型:
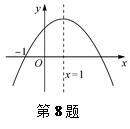
| A.a>0 | B.b>0 | C. c<0 | D.3不是方程ax2+bx+c=0的一个根 |
科目:czsx 来源:2012-2013学年北京市燕山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,已知△ABC中,∠C=90°,点D在边AC上,∠BDC=45°,BD=10 ,AC=10
,AC=10 ,求∠A的度数.
,求∠A的度数.
科目:czsx 来源: 题型:
| A.x=1时的函数值相等 | B.x=0时的函数值相等 |
C.x= 时的函数值相等 时的函数值相等 | D.x=- 时的函数值相等 时的函数值相等 |
科目:czsx 来源:2011-2012学年浙江省菁才中学八年级上学期期中考试数学试卷(带解析) 题型:解答题
如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的△DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转。
⑴在图1中,DE交AB于M,DF交BC于N。①说明DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
⑵继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出理由;若不成立,请说明理由;
⑶继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?若成立,请给出结论,不用说明理由。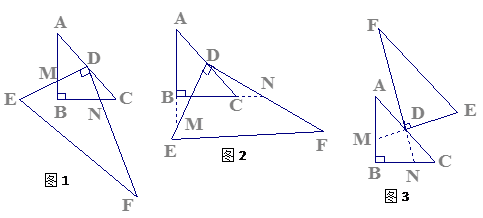
科目:czsx 来源:2012-2013学年福建泉州三中七年级上期末考试数学试卷(带解析) 题型:填空题
已知等式:2+ =22×
=22× ,3+
,3+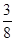 =32×
=32×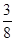 ,4+
,4+ =42×
=42× ,……,10+
,……,10+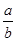 =102×
=102×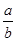 ,(a,b均为正整数),则a+b= .
,(a,b均为正整数),则a+b= .
科目:czsx 来源:2011年河北丰润区中考第一次模拟数学试卷 题型:选择题
如图,已知AD∥BC,∠B=30º,DB平分∠ADE,则∠CED的度数为( )

A.30º B.60º C.90º D.120º
科目:czsx 来源:2012年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:选择题
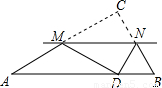
如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=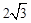 ,则四边形MABN的面积是【 】
,则四边形MABN的面积是【 】
A.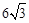 B.
B. C.
C. D.
D.
科目:czsx 来源:2015届浙江慈溪育才中学八年级上学期第二次月考数学试卷(解析版) 题型:解答题
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B.点C重合).

(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.
科目:czsx 来源: 题型:
(本题满分10分)(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等。
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
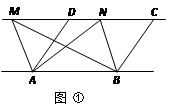
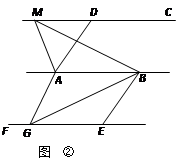
(2)结论应用:
如图③,抛物线![]() 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线![]() 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.


科目:czsx 来源:2013-2014学年江苏省无锡市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).

(1)求这个二次函数的关系式;
(2)若一次函数y=-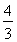 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
科目:czsx 来源:2012-2013学年福建泉州三中七年级上期末考试数学试卷(解析版) 题型:填空题
已知等式:2+ =22×
=22× ,3+
,3+ =32×
=32× ,4+
,4+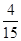 =42×
=42×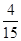 ,……,10+
,……,10+ =102×
=102× ,(a,b均为正整数),则a+b= .
,(a,b均为正整数),则a+b= .