精英家教网 >
试题搜索列表 >已知三角形abc和三角形cde中,ca=cb,cd=ce,角acb=角dce=α,ae与bd交于点f.1,当α=90
已知三角形abc和三角形cde中,ca=cb,cd=ce,角acb=角dce=α,ae与bd交于点f.1,当α=90答案解析
科目:czsx
来源:
题型:
已知:△ABC和△ADE都是等腰直角三角形,其中∠ABC=∠ADE=90°,点M为EC的中点.
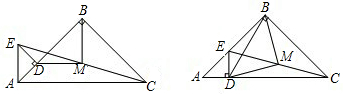
(1)如图,当点D,E分别在AC,AB上时,求证:△BMD为等腰直角三角形;
(2)如图,将图中的△ADE绕点A逆时针旋转45°,使点D落在AB上,此时问题(1)中的结论“△BMD为等腰直角三角形”还成立吗?请对你的结论加以证明.
查看答案和解析>>
科目:czsx
来源:
题型:
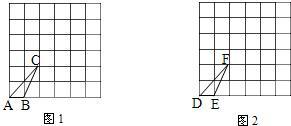
13、已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A
1B
1C
1,请你在图1中画出△A
1B
1C
1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
查看答案和解析>>
科目:czsx
来源:
题型:
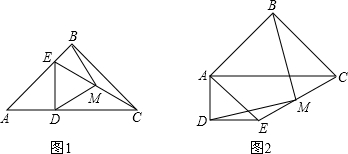
(2012•丰台区一模)已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA=BC,DA=DE,连接EC,取EC的中点M,连接BM和DM.
(1)如图1,如果点D、E分别在边AC、AB上,那么BM、DM的数量关系与位置关系是
BM=DM且BM⊥DM
BM=DM且BM⊥DM
;
(2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
25、已知:△ABC和△ADE均为等腰直角三角形,∠ABC=∠ADE=90°,AB=BC,AD=DE,按图1放置,使点E在BC上,取CE的中点F,连接DF、BF.
(1)探索DF、BF的数量关系和位置关系,并证明;
(2)将图1中△ADE绕A点顺时针旋转45°,再连接CE,取CE的中点F(如图2),问(1)中的结论是否仍然成立?证明你的结论;
(3)将图1中△ADE绕A点转动任意角度(旋转角在0°到90°之间),再连接CE,取CE的中点F(如图3),问(1)中的结论是否仍然成立?证明你的结论.

查看答案和解析>>
科目:czsx
来源:
题型:
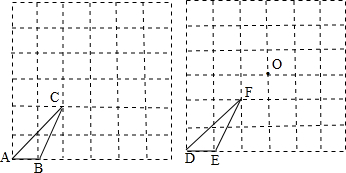
(2007•怀柔区二模)已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图中的格点,△ABC先向右平移3个单位,再向上平移2个单位,得到格点三角形A
1B
1C
1.请你在图1中画出A
1B
1C
1;
(2)在图中画一个格点△D
1E
1F
1,使格点△D
1E
1F
1与格点△DEF关于点O成中心对称.(说明:顶点都在网格线交点处的三角形叫做格点三角形)
查看答案和解析>>
科目:czsx
来源:
题型:
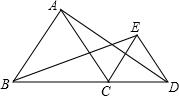
已知,△ABC和△CDE都是等边三角形,且点B,C,D在同一条直线上.求证:BE=AD.
查看答案和解析>>
科目:czsx
来源:
题型:
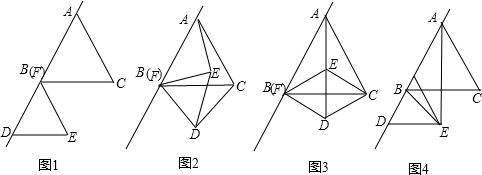
如图1,正△ABC和正△FDE,F与B重合,AB与FD在一条直线上.
(1)若将△FDE绕点B旋转一定角度(如图2),试说明CD=AE;
(2)已知AB=6,DE=
2,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
(3)若把图1中的正△FDE沿BA方向平移(如图4),连接AE、BE,已知正△ABC和正△FDE的边长分别是5cm和
2cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
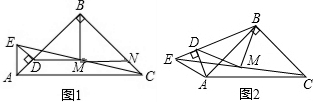
已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.
(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为
;
(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知图1和图2中,正方形的边长为1,按要求作格点三角形,并注相应的字母,
(1)在图1中作△ABC,使各其边长均为整数;
(2)在图2中作△A′B′C′,使△A′B′C′∽△ABC,并且A′B′:AB=
.

查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读:
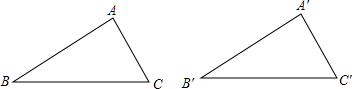
如图,已知在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,AC=A′C′.那么△ABC≌△A′B′C′.

说明过程如下:
把△ABC放到△A′B′C′上,使∠A的顶点与∠A′的顶点重合;由于∠A=∠A′,因此可以使射线AB、AC分别落在射线A′B′、A′C′上.因为AB=A′B′,AC=A′C′,所以点B、C分别与点B′、C′重合,这样△ABC和△A′B′C′重合,即△ABC≌△A′B′C′.
于是,得全等三角形判定方法1:在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S).
请完成下面问题的填空:
如图,已知在△ABC和△A′B′C′中,∠A=∠A′,AB=A′B′∠B=∠B′.
那么△ABC≌△A′B′C′.
说明过程如下:
把△ABC放到△A′B′C′上,因为AB=A′B′,可以使
AB
AB
与
A′B′
A′B′
重合,并使点C与C′在AB(A′B′)的同一侧,这时点A与点A′重合,点
C
C
与点
C′
C′
重合.由于∠A=∠A′,因此射线
AC
AC
与射线
A′C′
A′C′
叠合;由于
∠B=∠B′,因此射线
BC
BC
与射线
B′C′
B′C′
叠合.于是点C(射线AC与BC的交点)与点C(射线A′C′与B′C′的交点)重合.这样
△ABC
△ABC
与
△A′B′C′
△A′B′C′
重合,即△ABC≌△A′B′C′.
于是,得全等三角形判定方法2:在两个三角形中,
如果两角和它们的夹边对应相等,那么这两个三角形全等(简记为ASA)
如果两角和它们的夹边对应相等,那么这两个三角形全等(简记为ASA)
.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:关于x的一元二次方程: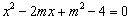 .
.
(1)求证:这个方程有两个不相等的实数根;
(2)当抛物线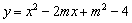 与x轴的交点位于原点的两侧,且到原点的距离相等时,
与x轴的交点位于原点的两侧,且到原点的距离相等时,
求此抛物线的解析式;
(3)将(2)中的抛物线在x轴下方的部分沿x轴翻折,其余部分保持能够不变,得到图形C1,将图形C1向右平移一个单位,得到图形C2,当直线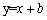 (b<0)与图形C2恰有两个公共点时,写出b的取值范围.
(b<0)与图形C2恰有两个公共点时,写出b的取值范围.
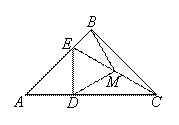
24.已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA=BC,DA=DE,联结EC,取EC的中点M,联结BM和DM.
(1)如图1,如果点D、E分别在边AC、AB上,那么BM、DM的数量关系与位置关系是 ;
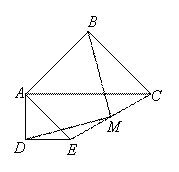 (2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.
(2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:czsx
来源:2005年初中毕业升学考试(江苏无锡卷)数学(带解析)
题型:解答题
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A1B1C1,请你在图1中画出△A1B1C1.
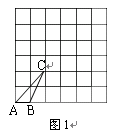
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
查看答案和解析>>
科目:czsx
来源:2005年初中毕业升学考试(江苏无锡卷)数学(解析版)
题型:解答题
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A1B1C1,请你在图1中画出△A1B1C1.

(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.

查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《图形的相似》(07)(解析版)
题型:解答题
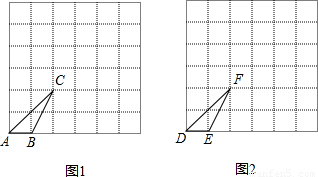
(2005•无锡)已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A
1B
1C
1,请你在图1中画出△A
1B
1C
1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
查看答案和解析>>
科目:czsx
来源:第4章《相似三角形》中考题集(28):4.4 相似三角形的性质及其应用(解析版)
题型:解答题
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A
1B
1C
1,请你在图1中画出△A
1B
1C
1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.

查看答案和解析>>
科目:czsx
来源:2007年北京市怀柔区中考数学二模试卷(解析版)
题型:解答题
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图中的格点,△ABC先向右平移3个单位,再向上平移2个单位,得到格点三角形A
1B
1C
1.请你在图1中画出A
1B
1C
1;
(2)在图中画一个格点△D
1E
1F
1,使格点△D
1E
1F
1与格点△DEF关于点O成中心对称.(说明:顶点都在网格线交点处的三角形叫做格点三角形)

查看答案和解析>>
科目:czsx
来源:
题型:
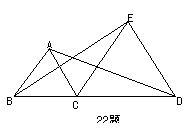
已知,△ABC和△CDE都是等边三角形,且点B,C,D在同一条直线上。求证:BE=AD。
查看答案和解析>>
科目:czsx
来源:2008年四川省绵阳市南山中学自主招生考试数学试卷(解析版)
题型:解答题
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A
1B
1C
1,请你在图1中画出△A
1B
1C
1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.

查看答案和解析>>
科目:czsx
来源:第25章《图形的变换》中考题集(05):25.1 平移变换(解析版)
题型:解答题
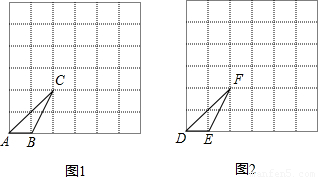
已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A
1B
1C
1,请你在图1中画出△A
1B
1C
1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
查看答案和解析>>
科目:czsx
来源:南长区二模
题型:解答题
已知图1和图2中,正方形的边长为1,按要求作格点三角形,并注相应的字母,
(1)在图1中作△ABC,使各其边长均为整数;
(2)在图2中作△A′B′C′,使△A′B′C′
∽△ABC,并且A′B′:AB=
.

查看答案和解析>>


 13、已知图1和图2中的每个小正方形的边长都是1个单位.
13、已知图1和图2中的每个小正方形的边长都是1个单位.







![]() .
.![]() 与x轴的交点位于原点的两侧,且到原点的距离相等时,
与x轴的交点位于原点的两侧,且到原点的距离相等时,![]() (b<0)与图形C2恰有两个公共点时,写出b的取值范围.
(b<0)与图形C2恰有两个公共点时,写出b的取值范围.  (2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.
(2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由. 









