
题目列表(包括答案和解析)
已知:如图,∠AOB=30°,M为OB上一点,OM=5 cm,且以M为圆心,r为半径的圆与直线OA有什么样的位置关系?

(1)r=2 cm;(2)r=4 cm;(3)r=2.5 cm.
已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,Ð DOC=2Ð ACD=90°.

(1)求证:直线AC是圆O的切线;
(2)如果Ð ACB=75°,圆O的半径为2,求BD的长.
已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F
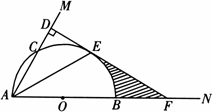
(1)猜想ED与⊙O的位置关系,并说明理由;
(2)若cos∠MAN=![]() ,AE=
,AE=![]() ,求阴影部分的面积
,求阴影部分的面积
| |||||||||||
如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于A、B两点,以OA为直径作半圆,圆心为D。M是OB上一动点(不运动到O点、B点),过M点作半圆的切线交直线
轴分别交于A、B两点,以OA为直径作半圆,圆心为D。M是OB上一动点(不运动到O点、B点),过M点作半圆的切线交直线![]() 于N,交AB于F,切点为P。连结DN交AB于E,连结DM。
于N,交AB于F,切点为P。连结DN交AB于E,连结DM。
(
1)证明:∠OMD=∠ADN;(
2)设OM(
3)当以A、F、N为顶点的三角形与△ADE相似时,求直线MN的解析式。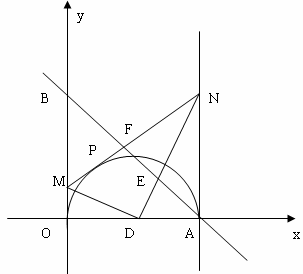
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com