
题目列表(包括答案和解析)
 两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形;
两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则 ;
;给出下列命题:
①已知椭圆 两焦点
两焦点 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点 ,使得△
,使得△ 为直角三角形;
为直角三角形;
②已知直线 过抛物线
过抛物线 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于 两点,则
两点,则 的最小值为2;
的最小值为2;
③若过双曲线 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为 为坐标原点,则
为坐标原点,则 ;
;
④根据气象记录,知道荆门和襄阳两地一年中雨天所占的概率分别为20%和18%,两地同时下雨的概率为12%,则荆门为雨天时,襄阳也为雨天的概率是60%.
其中正确命题的序号是( )
A.①③④ B.①②③ C.③④ D.①②④
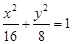 两焦点
两焦点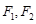 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点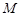 ,使得△
,使得△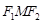 为直角三角形;
为直角三角形;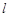 过抛物线
过抛物线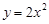 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于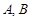 两点,则
两点,则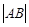 的最小值为2;
的最小值为2;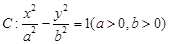 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为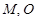 为坐标原点,则
为坐标原点,则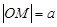 ;
;| A.①③④ | B.①②③ | C.③④ | D.①②④ |
 =1两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形;
=1两焦点F1,F2,则椭圆上存在六个不同点M,使得△F1MF2为直角三角形; =1(a>0,b>0)的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
=1(a>0,b>0)的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;| x2 |
| 16 |
| y2 |
| 8 |
| x2 |
| a2 |
| y2 |
| b2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com