
题目列表(包括答案和解析)
(本小题满分12分)请你设计一个包装盒,如下图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(cm).

(I)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.[
(本小题满分12分)
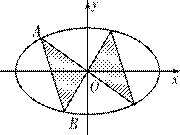
某公园的大型中心花园的边界为椭圆,花园内种植各种花草. 为增强观赏性,在椭圆内以其
中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草(如图),并以该直角三角
形斜边开辟观赏小道(其中的一条为线段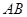 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,
在施工时发现,椭圆边界上任意一点到椭圆两焦点的距离和为4(单位:百米),且椭圆上点
到焦点的最近距离为1(单位:百米).
(Ⅰ)以椭圆中心为原点建立如图的坐标系,求该椭圆的标准方程;
(Ⅱ)请计算观赏小道的长度(不计小道宽度)的最大值.
 |
(本小题满分12分)
某公园的大型中心花园的边界为椭圆,花园内种植各种花草. 为增强观赏性,在椭圆内以其
中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草(如图),并以该直角三角
形斜边开辟观赏小道(其中的一条为线段![]() ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,
在施工时发现,椭圆边界上任意一点到椭圆两焦点的距离和为4(单位:百米),且椭圆上点
到焦点的最近距离为1(单位:百米).
 (Ⅰ)以椭圆中心为原点建立如图的坐标系,求该椭圆的标准方程;
(Ⅰ)以椭圆中心为原点建立如图的坐标系,求该椭圆的标准方程;
(Ⅱ)请计算观赏小道的长度(不计小道宽度)的最大值.
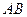 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设, |
(本小题满分12分)请你设计一个包装盒,如下 图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(
图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x( cm).
cm).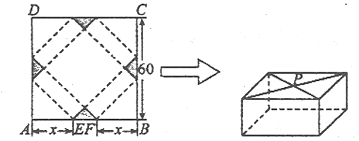
(I)某广告商要求包装盒的侧面积S(cm2) 最大,试问x应取何值?
最大,试问x应取何值?
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.[
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com