
题目列表(包括答案和解析)
 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为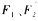 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形 是边长为2的正方形.
是边长为2的正方形.
 圆的方程;
圆的方程; 为定值;
为定值; 过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.
过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.(本小题满分13分) 已知过点(1,0)的直线![]() 相交于P、Q两点,PQ中点坐标为
相交于P、Q两点,PQ中点坐标为![]() (O为坐标原点)。 (I)求直线
(O为坐标原点)。 (I)求直线![]() 的方程; (II)证明:
的方程; (II)证明:![]() 为定值。
为定值。
(本小题满分13分)
若A、B是抛物线y2=4x上的不同两点,弦AB(不平行于y轴)的垂直平分线与
x轴相交于点P,则称弦AB是点P的一条“相关弦”.已知当x>2时,点P(x,0)
存在无穷多条“相关弦”.给定x0>2.
(I)证明:点P(x0,0)的所有“相关弦”的中点的横坐标相同;
(II) 试问:点P(x0,0)的“相关弦”的弦长中是否存在最大值?
若存在,求其最大值(用x0表示):若不存在,请说明理由.
(本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组![]() ;第二组
;第二组![]() ,……,第五组
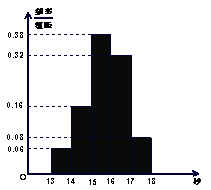
,……,第五组![]() .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设![]() 、
、![]() 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
(本小题满分12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组![]() ;第二组
;第二组![]() ,……,第五组
,……,第五组![]() .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设![]() 、
、![]() 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com