（本小题满分1 2分）

    甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子，乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子．

  （1）若甲在自己的箱子里任意取球，取后不放回，每次只取一球，直到取得红球为止，求甲取球次数的数学期望；

（2）若甲、乙两人各自从自己的箱子里任取一球比颜色，规定同色时为甲胜，异色时为乙胜，这个游戏规则公平吗？请说明理由．

（本小题满分12分）

某校游园活动有这样一个游戏项目：甲箱子里装有3个白球、2个黑球，乙箱子里装有1个白球、2个黑球，这些球除颜色外完全相同，每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖．（每次游戏结束后将球放回原箱）

（Ⅰ）求在1次游戏中，

（i）摸出3个白球的概率；（ii）获奖的概率；

（Ⅱ）求在2次游戏中获奖次数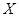的分布列及数学期望.       

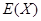（本小题满分16分）
如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的半径都是2km，点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形活动场地．
（1）如图甲，要建的活动场地为△RST，求场地的最大面积；
（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．

（本小题满分12分）品厂为了检查甲、乙两条自动包装流水线的生产情况，在这两条

   流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]

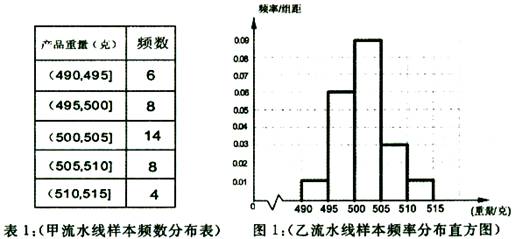
   的产品为合格品，否则为不合格品，表1是甲流水线样本频数分布表，图1是乙流水线样

   本的频率分布直方图。

某食

（1）若检验员不小心将甲、乙两条流水线生产的重量值在（510，515]的产品放在了一起，

      然后又随机取出3件产品，求至少有一件是乙流水线生产的产品的概率；

 （2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量

      与两条自动包装流水线的选择有关”。

（本小题满分12分）．在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，

现从甲、乙两个盒子中各取出1个球，每个小球被取出的可能性相等

（I）求取出的两个球上标号为相邻整数的概率；

（II）求取出的两个球上标号之和能被3整除的概率.