
题目列表(包括答案和解析)
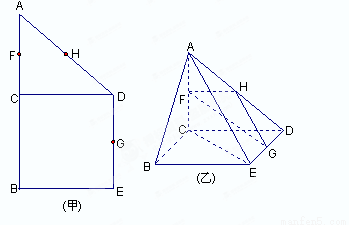
(本小题满分13分)如图(甲),在直角梯形ABED中,AB//DE,AB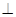 BE,AB
BE,AB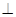 CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分别为AC ,AD ,DE的中点,现将△ACD沿CD折起,使平面ACD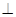 平面CBED,如图(乙).
平面CBED,如图(乙).
(1)求证:平面FHG//平面ABE;
(2)记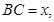
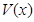 表示三棱锥B-ACE
的体积,求
表示三棱锥B-ACE
的体积,求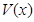 的最大值;
的最大值;
(3)当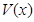 取得最大值时,求二面角D-AB-C的余弦值.
取得最大值时,求二面角D-AB-C的余弦值.
(本小题满分12分)
甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹。根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2。
设甲、乙的射击相互独立。
(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;
(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率。
(本小题满分12分)
为了预防春季流感,市防疫部门提供了编号为1,2,3,4的四种疫苗供市民选择注射,每个人均能从中任选一个编号的疫苗接种,现有甲,乙,丙三人接科苗.
(I )求三人注射的疫苗编号互不相同的概率;
(II)设三人中选择的疫苗编号最大数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)(考生注意:本题请从以下甲乙两题中任选一题作答,若两题都答 只以甲题计分)
甲:设数列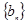 的前
的前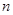 项和为
项和为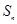 ,且
,且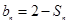 ;数列
;数列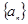 为等差数列,且
为等差数列,且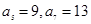
(Ⅰ)求数列 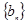 的通项公式
的通项公式
(Ⅱ)若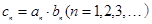 ,
, 为数列
为数列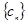 的前
的前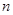 项和,求
项和,求
乙:定义在[-1,1]上的奇函数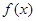 ,已知当
,已知当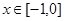 时,
时,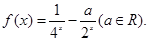
(Ⅰ)求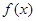 在[0,1]上的最大值
在[0,1]上的最大值
(Ⅱ)若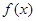 是[0,1]上的增函数,求实数
是[0,1]上的增函数,求实数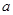 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com