
题目列表(包括答案和解析)
(本小题满分12分)已知某校5个学生的数学和物理成绩如下表
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学 | 80 | 75 | 70 | 65 | 60 |
| 物理 | 70 | 66 | 68 | 64 | 62 |
(1)假设在对这![]() 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这![]() 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有![]() 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 与
与![]() 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在![]() 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式:![]() ,其中
,其中 ,
,![]() ;
;![]() ,残差和公式为:
,残差和公式为:![]()
(本小题满分12分)已知某校5个学生的数学和物理成绩如下表
| 学生的编号 | 1 | 2 | 3 | 4 | 5 |
| 数学 | 80 | 75 | 70 | 65 | 60 |
| 物理 | 70 | 66 | 68 | 64 | 62 |
(1)假设在对这![]() 名学生成绩进行统计时,把这
名学生成绩进行统计时,把这![]() 名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有
名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有![]() 名学生的物理成绩是自己的实际分数的概率是多少?
名学生的物理成绩是自己的实际分数的概率是多少?
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 与
与![]() 的回归方程;
的回归方程;
(3)利用残差分析回归方程的拟合效果,若残差和在![]() 范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”.
参考数据和公式:![]() ,其中
,其中 ,
,![]() ;
;![]() ,残差和公式为:
,残差和公式为:![]()
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
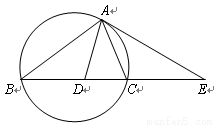
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:![]() 。
。

B.选修4—2 矩阵与变换
在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系![]() 中,点
中,点![]() 是椭圆
是椭圆![]() 上的一个动点,求
上的一个动点,求![]() 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:![]() 。
。
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。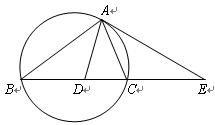 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 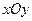 中,设椭圆 中,设椭圆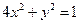 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 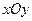 中,点 中,点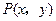 是椭圆 是椭圆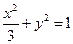 上的一个动点,求 上的一个动点,求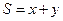 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
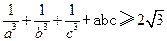 。
。从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证: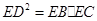 。
。
B.选修4—2 矩阵与变换
在平面直角坐标系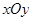 中,设椭圆
中,设椭圆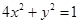 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系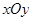 中,点
中,点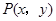 是椭圆
是椭圆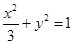 上的一个动点,求
上的一个动点,求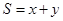 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证: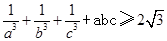 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com