
题目列表(包括答案和解析)
(本小题满分13分)某厂用甲、乙两种产品,已知生产1吨A产品,1吨B产品分别需要的甲乙原料数、可获得的利润及该厂现有原料数如表:
产品 所需原料 | A产品(t) | B产品(t) | 现有原料(t) |
甲(t) | 2 | 1 | 14 |
乙(t) | 1 | 3 | 18 |
利润(万元) | 5 | 3 |
|
(1)在现有原料下,A、B产品应各生产多少才能使利润最大?
(2)如果1吨B产品的利润增加到20万元,原来的最优解为何改变?
(3)如果1吨B产品的利润减少1万元,原来的最优解为何改变?
(4)1吨B产品的利润在什么范围,原最优解才不会改变?
(本小题满分13分)
在一次数学考试中,共有10道选择题,每题均有四个选项,其中有且只有一个选项是正确的,评分标准规定:“每道题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有6道题是正确的,其余题目中:有两道题可判断两个选项是错误的,有一道可判断一个选项是错误的,还有一道因不理解题意只好乱猜,请求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)设该考生所得分数为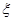 ,求
,求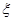 的数学期望.
的数学期望.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解,训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61—70 分 | 71—80 分 | 81-90 分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(I )试分别估计两个班级的优秀率;
(II)由以上统计数据填写下面2 X 2列联表,并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对提商‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据:![]() ,
,
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0. 05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
(本小题满分13分)
已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,若函数
,若函数![]() 与
与![]() 轴有两个交点,求实数
轴有两个交点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)证明:曲线![]() 上任意一点的切线与直线
上任意一点的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求出此定值.
所围成的三角形面积为定值,并求出此定值.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解,训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61—70 分 | 71—80 分 | 81-90 分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(I )试分别估计两个班级的优秀率;
(II)由以上统计数据填写下面2 X 2列联表,并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对提商‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据:![]() ,
,
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0. 05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com