某地一经济适用房楼盘一楼是商铺（暂不出售），二楼至二十三楼均为商品适用房（对外出售）．商品房售价方案如下：第八层售价为2000元/m²，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元．已知商品房每套面积均为80平方米．开发商为购买者制定了两种购买方案：
方案一：购买者先交纳首付金额（商品房总价的30%），再办理分期付款（即贷款）．
方案二：购买者一次性付清所有房款，则享受8%的优惠，并免收五年物业管理费（已知每月物业管理费为a元）
（1）请写出每平方米售价y（元/米²）与楼层x（2≤x≤23，x是正整数）之间的函数关系式；
（2）王老师已筹到60000元，若用方案一购房，他可以购买哪些楼层的商品房呢？
（3）有人建议王老师使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算．你认为王老师的说法一定正确吗？请通过运算确定a的范围，阐明你的看法．

某地一经济适用房楼盘一楼是商铺（暂不出售），二楼至二十三楼均为商品适用房（对外出售）．商品房售价方案如下：第八层售价为2000元/m²，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元．已知商品房每套面积均为80平方米．开发商为购买者制定了两种购买方案：
方案一：购买者先交纳首付金额（商品房总价的30%），再办理分期付款（即贷款）．
方案二：购买者一次性付清所有房款，则享受8%的优惠，并免收五年物业管理费（已知每月物业管理费为a元）
（1）请写出每平方米售价y（元/米²）与楼层x（2≤x≤23，x是正整数）之间的函数关系式；
（2）王老师已筹到60000元，若用方案一购房，他可以购买哪些楼层的商品房呢？
（3）有人建议王老师使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算．你认为王老师的说法一定正确吗？请通过运算确定a的范围，阐明你的看法．

（2013•郑州模拟）某地一经济适用房楼盘一楼是商铺（暂不出售），二楼至二十三楼均为商品适用房（对外出售）．商品房售价方案如下：第八层售价为2000元/m²，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元．已知商品房每套面积均为80平方米．开发商为购买者制定了两种购买方案：
方案一：购买者先交纳首付金额（商品房总价的30%），再办理分期付款（即贷款）．
方案二：购买者一次性付清所有房款，则享受8%的优惠，并免收五年物业管理费（已知每月物业管理费为a元）
（1）请写出每平方米售价y（元/米²）与楼层x（2≤x≤23，x是正整数）之间的函数关系式；
（2）王老师已筹到60000元，若用方案一购房，他可以购买哪些楼层的商品房呢？
（3）有人建议王老师使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算．你认为王老师的说法一定正确吗？请通过运算确定a的范围，阐明你的看法．

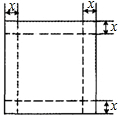
如图，一张边长为20cm正方形硬纸板，把它的四个角都剪去一个边长为xcm的小正方形，然后把它折成一个无盖的长方体，设长方体的容积为Vcm³，请回答下列问题：
（1）若用含有x的代数式表示V，则V=．
（2）根据（1）中结果，填写下表：

x（cm）	1	2	3	4	5	6	7
V（cm3）	324	512			500	384	252

（3）观察（2）中表格，容积V的值是否随x值的增大而增大？此时当x取什么整数值时，容积V的值最大？
（4）课后小英同学继续对这个问题作了以下探究：
当x=3.2cm时，V=591.872cm³；当x=3.3cm时，V=592.548cm³；
当x=3.4cm时，V=592.416cm³；当x=3.5cm时，V=591.5cm³，
小英同学发现x的取值一定介于3.3cm～3.4cm之间，估计x的取值还能更精确些，小英再计算x=3.3cm，3.33cm，3.333cm，3.3333cm…时，发现容积还在逐渐增大．现请你也观察（4）中数据变化，能否推测x可以取到哪一个定值，容积V的值最大？（直接写出即可）