
题目列表(包括答案和解析)
【答案】0<m<2.
【考点】二次函数的图象;反比例函数的图象.
【专题】图表型.
【分析】首先作出分段函数y=![]() 的图象,根据函数的图象即可确定m的取值范围.
的图象,根据函数的图象即可确定m的取值范围.
 【解答】分段函数y=
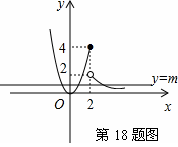
【解答】分段函数y=![]() 的图象如右图所示:
的图象如右图所示:
故要使直线y=m(m为常数)与函数y=![]() 的图象恒有三个不同的交点,常数m的取值范围为0<m<2,
的图象恒有三个不同的交点,常数m的取值范围为0<m<2,
故答案为:0<m<2.
【点评】本题考查了二次函数的图象及反比例函数的图象,首先作出分段函数的图象是解决本题的关键,采用数形结合的方法确定答案是数学上常用的方法之一.
|
【解析】本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系
|
 的方程
的方程 ,
, 是实数.(1)试判定该方程根的情况;(2)若已知
是实数.(1)试判定该方程根的情况;(2)若已知
 ,且该方程的两根都是整数,求
,且该方程的两根都是整数,求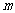 的值.
的值.
【解析】本题考查了一元二次方程的根的判别式.一元二次方程根的情况与判别式△的关系
| 2b+3c |
| a |
| 2a+3c | a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com