12．解:⑴设A(.0).B(.0).由题设可求得C点的坐标为(0.).且＜0. ＞0.∵＜0.∴＞0 由S△AOC-S△BOC＝OA·OB得: 得: 得: ⑵设抛物线的对称轴与轴交于点M.与△PAB的外接圆交于点N. ∵tan∠CAB=.∴.∴A点的坐标为(.0) ∴A点在抛物线上. ∴.代入.得又 ∵.为方程的两根. ∴.即: ∴ ∴B点的坐标为(.0). ∴顶点P的坐标为(.) 由相交弦定理得: AM·BM=PM·MN 又 ∵. ∴AM=BM=.PM= ∴. ∴. ∴所求的抛物线的函数解析式是: 【查看更多】

本题分为A、B 两类题，你可从A、B 两类题中任选一题解答即可
（A类）：如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求四边形AQMP的周长；
（2）写出图中的两对相似三角形（不需证明）；
（3）M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由．
（B类）：有人这样证明三角形内角和是180°，如图，D是△ABC内一点，连接AD、BD、CD，他们将△ABC分成了三个小的三角形．因此有：三个小三角形的内角和的和比△ABC的内角和多360°，如果设三角形内角

和是x，则有：x+x+x=x+360°，易解得x=180°，你认为这个证明正确吗？说说你的理由．

查看答案和解析>>

本题分为A、B 两类题，你可从A、B 两类题中任选一题解答即可
（A类）：如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
（1）求四边形AQMP的周长；
（2）写出图中的两对相似三角形（不需证明）；
（3）M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由．
（B类）：有人这样证明三角形内角和是180°，如图，D是△ABC内一点，连接AD、BD、CD，他们将△ABC分成了三个小的三角形．因此有：三个小三角形的内角和的和比△ABC的内角和多360°，如果设三角形内角和是x，则有：x+x+x=x+360°，易解得x=180°，你认为这个证明正确吗？说说你的理由．

查看答案和解析>>

查看答案和解析>>

如图，A、B两点被池塘隔开，为测量AB两点的距离，如图①在AB外选一点C，联结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN＝20 m，那么AB＝________．

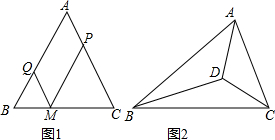
(1)测AB距离也可由图②所示用三角形全等的知识来解决，请根据题意填空：延长AC到D，使CD＝AC，延长BC到E，使CE＝________，则由全等三角形得，AB＝________．

(2)测AB距离还可以用其他的几何知识来设计测量方案，求出AB的长．请你在图③中画出图形，并叙述你的测量方案．

查看答案和解析>>

如图1，A、B两点被池塘隔开，为测量AB两点的距离，在AB外选一点C，连接AC和BC，并分别找出AC和BC的中点M、N，则MN是△ABC的中位线，根据三角形的中位线定理：三角形的中位线平行于第三边且等于第三边的一半，如果测得MN=20m，那么AB=2×20m=40m．
（1）小红说：测AB距离也可以由图2所示用三角形全等知识来解决，请根据题意填空：延长AC到D，使CD=

AC

，延长BC到E，使CE=

BC

，由全等三角形得，AB=ED；
（2）小华说：测AB距离也可以由三角形相似的知识来设计测量方法，求出AB的长；请根据题意在如图3中画出相应的测量图形：延长AC到H，使CH=2AC，延长BC到Q，使CQ=2BC，连接QH；若测得QH的长是400米，你能测出AB的长吗？若能，请测出；若不能，请说明理由．

查看答案和解析>>

练习册

高中

初中

小学