
题目列表(包括答案和解析)
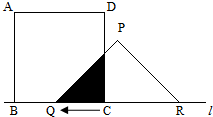 头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题:
头所示方向开始匀速运动,t秒后正方形ABCD与等腰△PQR重合部分的面积为Scm2.解答下列问题: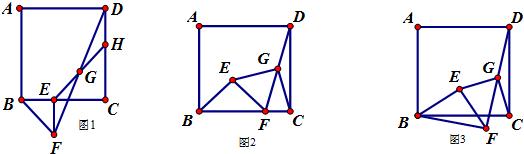
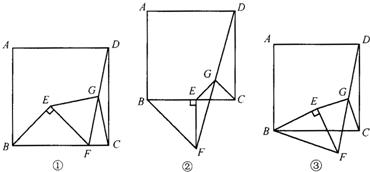
 已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点F在BC上,取DF的中点G,连接EG,CG.试探究EG,CG的位置关系与数量关系并证明.
已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点F在BC上,取DF的中点G,连接EG,CG.试探究EG,CG的位置关系与数量关系并证明.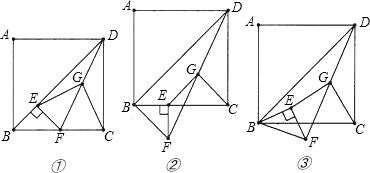
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com