如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE.我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系：

　　(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系(直接写出答案)；

　　②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α得到图2，图3的情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断.

　　(2)在第(1)题图2中，连接DG、BE，且AB=3，EF=2，求BE2+DG2的值.

如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE.我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系：

　　(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系(直接写出答案)；
　　②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α得到图2，图3的情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断.
　　(2)在第(1)题图2中，连接DG、BE，且AB=3，EF=2，求BE2+DG2的值.

如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE.我们探究下列图中线段BG、DE的长度关系及所在直线的位置关系：

　　(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系(直接写出答案)；

　　②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α得到图2，图3的情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并选取图2证明你的判断.

　　(2)在第(1)题图2中，连接DG、BE，且AB=3，EF=2，求BE2+DG2的值.

阅读下面的材料：

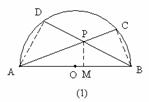
如图（1），在以AB为直径的半圆O内有一点P，AP、BP的延长线分别交半圆O于点C、D．

求证：AP?AC+BP?BD=AB²．

证明：连结AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90^ｏ，

∴点D、M在以AP为直径的圆上；同理：M、C在以BP为直径的圆上．

由割线定理得： AP?AC=AM?AB，BP?BD=BM?BA，

所以，AP?AC+BP?BD=AM?AB+BM?AB=AB?（AM+BM）=AB²．

　当点P在半圆周上时，也有AP?AC+BP?BD=AP²+BP²=AB²成立，那么：

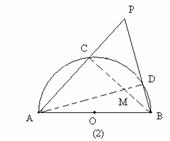
（1）如图（2）当点P在半圆周外时，结论AP?AC+BP?BD=AB²是否成立？为什么？

（2）如图（3）当点P在切线BE外侧时，你能得到什么结论？将你得到的结论写出来．

阅读下面的材料：

如图（1），在以AB为直径的半圆O内有一点P，AP、BP的延长线分别交半圆O于点C、D．求证：AP·AC+BP·BD=AB²．

证明：连结AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90ｏ，

∴点D、M在以AP为直径的圆上；同理：M、C在以BP为直径的圆上．

由割线定理得： AP·AC=AM·AB，BP·BD=BM·BA，

所以，AP·AC+BP·BD=AM·AB+BM·AB=AB·（AM+BM）=AB2．

　当点P在半圆周上时，也有AP·AC+BP·BD=AP2+BP2=AB2成立，那么：

(1）如图（2）当点P在半圆周外时，结论AP·AC+BP·BD=AB2是否成立？为什么？

(2）如图（3）当点P在切线BE外侧时，你能得到什么结论？将你得到的结论写出来．