
题目列表(包括答案和解析)
考试结束,请将本试题卷和答题卡一并上交。
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集![]() ,集合
,集合![]() ,
,![]() ,则图中的阴影部分表示的集合为
,则图中的阴影部分表示的集合为
 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知非零向量![]() 、
、![]() 满足
满足![]() ,那么向量
,那么向量![]() 与向量
与向量![]() 的夹角为
的夹角为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.![]() 的展开式中第三项的系数是
的展开式中第三项的系数是
A.![]() B.
B.![]() C.15 D.
C.15 D.![]()
4.圆![]() 与直线
与直线![]() 相切于点
相切于点![]() ,则直线
,则直线![]() 的方程为
的方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| n |
 |
| k=1 |
根据角的终边要求写出角的集合
(1)

(2)

(3)、终边是直角坐标系中第二、四象限的角平分线
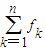
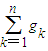 的最大值,并写出相应得一个排列
的最大值,并写出相应得一个排列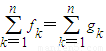 .
.由所有既属于集合A又属于集合B的元素所成的集合,叫做A与B的________,记作A∩B,即A∩B={x|x∈A,且x∈B}.
可这样理解:交集A∩B是由两集合A与B的“公有”元素所组成的集合.用Venn图表示,如图.

易知:(1)若两集合A与B无公共关系,则A∩B=________;
(2)A∩B________A,A∩B________B;
(3)A∩A=________,A∩![]() =________,A∩B=B∩A;
=________,A∩B=B∩A;
(4)若A![]() B,则A∩B=________;若A∩B=A,则A________B;
B,则A∩B=________;若A∩B=A,则A________B;
(5)设U为全集,则A∩(![]() A)=________.
A)=________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com