
题目列表(包括答案和解析)
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
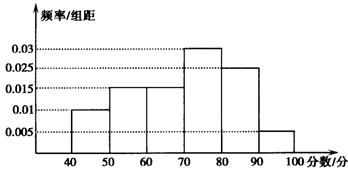
⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
【解析】本试题主要考查了统计和概率的综合运用。
第一问频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
第二问0.015×10+0.025×10+0.03×10+0.005×10=0.75
解:(1)频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75
为了了解某市工人开展体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,计算这2个工厂中至少有1个来自A区的概率.
【解析】本试题主要考查了统计和概率的综合运用。
第一问工厂总数为18+27+18=63,样本容量与总体中的个体数比为7/63=1/9…3分
所以从A,B,C三个区中应分别抽取的工厂个数为2,3,2。
第二问设A1,A2为在A区中的抽得的2个工厂,B1,B2,B3为在B区中抽得的3个工厂,
C1,C2为在C区中抽得的2个工厂。
这7个工厂中随机的抽取2个,全部的可能结果有1/2*7*6=32种。
随机的抽取的2个工厂至少有一个来自A区的结果有A1,A2),A1,B2),A1,B1),
A1,B3)A1,C2),A1,C1), …………9分
同理A2还能给合5种,一共有11种。
所以所求的概率为p=11/21
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
每次抛掷一枚骰子(六个面上分别标以数字![]()
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
本小题主要考查概率的基本知识,运用数学知识解决实际问题的能力。满分12分。
(本小题满分13分)
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【命题意图】本小题主要考查直线、椭圆等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com