
题目列表(包括答案和解析)
下列五种说法:①三个不同平面将空间最多分成![]() 个区域;②已知随机变量
个区域;②已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() ;③将三进制数字
;③将三进制数字![]() 化为十进制所得的数为
化为十进制所得的数为![]() ;④在一个
;④在一个![]() 列联表中,计算得到
列联表中,计算得到![]() 的观测值
的观测值![]() ,则其中两个变量间有关系的可能性为
,则其中两个变量间有关系的可能性为![]() %;⑤椭圆
%;⑤椭圆![]() 中,若半焦距
中,若半焦距![]() ,记
,记![]() 为焦点,则椭圆上仅存在四个点
为焦点,则椭圆上仅存在四个点![]() ,使得
,使得![]() .你认为说法错误的是:
.你认为说法错误的是:
| 8 |
| 15 |
| 1 |
| 15 |
(本小题满分13分)
有一种新型的奇强洗衣液,特点是去污速度快.已知每投放![]() ,且
,且![]() 个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中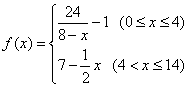 .若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
.若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若只投放一次![]() 个单位的洗衣液,2分钟时水中洗衣液的浓度为3(克/升),求
个单位的洗衣液,2分钟时水中洗衣液的浓度为3(克/升),求![]() 的值?
的值?
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
(3)若第一次投放2个单位的洗衣液,10分钟后再投放1个单位的洗衣液,在第12分
钟时洗衣液是否还能起到有效去污的作用?能,请加以证明;不能,请说明理由.
 ,
, 为互相垂直的单位向量,
为互相垂直的单位向量, =
= -2
-2 ,
, =
= +λ
+λ ,且
,且 ,
, 的夹角为锐角,则实数λ的取值范围是(-∞,
的夹角为锐角,则实数λ的取值范围是(-∞, );
); =10x+200;
=10x+200;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com