(本小题满分14分)

已知等差数列的公差不为零，首项且前项和为.

  （I）当时,在数列中找一项,使得成为等比数列,求的值.

  （II）当时，若自然数满足并且是等比数列，求的值。

(本小题满分14分)

已知等差数列的公差不为零，首项且前项和为.

  （I）当时,在数列中找一项,使得成为等比数列,求的值.

  （II）当时，若自然数满足并且是等比数列，求的值。

（本小题满分14分）
若由数列生成的数列满足对任意的其中
，则称数列为“Z数列”。
（I）在数列中，已知，试判断数列是否为“Z数列”；
（II）若数列是“Z数列”，
（III）若数列是“Z数列”，设求证

（本小题满分14分）

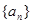        若由数列生成的数列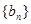满足对任意的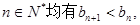其中[来源:Zxxk.Com]

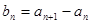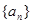，则称数列为“Z数列”。

   （I）在数列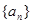中，已知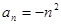，试判断数列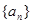是否为“Z数列”；

   （II）若数列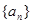是“Z数列”，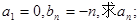

   （III）若数列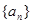是“Z数列”，设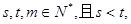求证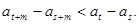

（本小题满分14分）

       随着科学技术的不断发展，人类通过计算机已找到了630万位的最大质数．陈成在学习中发现由41，43，47，53，61，71，83，97组成的数列中每一个数都是质数，他根据这列数的一个通项公式，得出了数列的后几项，发现它们也是质数．于是他断言：根据这个通项公式写出的数均为质数．

  （I）请你求出这个通项公式；

  （Ⅱ）从这个通项公式举出一个反例，说明陈成的说法是错误的．