
题目列表(包括答案和解析)
根据指令(r,![]() )(r≥0,-180°<
)(r≥0,-180°<![]() ≤180°),机器人在平面上能完成下列动作:先原地旋转角度
≤180°),机器人在平面上能完成下列动作:先原地旋转角度![]() (按逆时针方向旋转,
(按逆时针方向旋转,![]() 为正;按顺时针方向旋转,
为正;按顺时针方向旋转,![]() 为负),再朝其面对的方向沿直线行走距离r.
为负),再朝其面对的方向沿直线行走距离r.
(1)机器人位于直角坐标系的坐标原点,且面对x轴正方向,试给机器人下一个指令,使其移动到点(4,4);
(2)机器人在完成(1)中的指令后,发现在点(17,0)处有一小球正向坐标原点匀速直线滚动.已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令.(取cos81.87°=![]() )
)
已知直线ax+by=1中的a、b是取自集合{-3,-2,-1,0,1![]() ,2}中的2个元素,并且直线的倾斜角大于60°,那么符合这些条件的直线共有多少条?
,2}中的2个元素,并且直线的倾斜角大于60°,那么符合这些条件的直线共有多少条?
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(1)求f(x)的解析式;
(2)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。第一问,利用函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3,得到c=-3 ∴a=1, f(x)=x3-3x
(2)中设切点为(x0,x03-3x0),因为过点A(2,m),所以∴m-(x03-3x0)=(3x02-3)(2-x0)分离参数∴m=-2x03+6x02-6
然后利用g(x)=-2x3+6x2-6函数求导数,判定单调性,从而得到要是有三解,则需要满足-6<m<2
解:(1)f′(x)=3ax2+2bx+c
依题意
又f′(0)=-3
∴c=-3 ∴a=1 ∴f(x)=x3-3x
(2)设切点为(x0,x03-3x0),
∵f′(x)=3x2-3,∴f′(x0)=3x02-3
∴切线方程为y-(x03-3x0)=(3x02-3)(x-x0)
又切线过点A(2,m)
∴m-(x03-3x0)=(3x02-3)(2-x0)
∴m=-2x03+6x02-6
令g(x)=-2x3+6x2-6
则g′(x)=-6x2+12x=-6x(x-2)
由g′(x)=0得x=0或x=2
∴g(x)在(-∞,0)单调递减,(0,2)单调递增,(2,+∞)单调递减.
∴g(x)极小值=g(0)=-6,g(x)极大值=g(2)=2
画出草图知,当-6<m<2时,m=-2x3+6x2-6有三解,
所以m的取值范围是(-6,2).

两县城A和B相距20 km,现计划在两县城外以AB为直径的半圆弧![]() 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在![]() 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
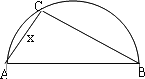
(1)按下列要求建立函数关系式:
(i)设∠CBA=![]() (rad),将y表示成
(rad),将y表示成![]() 的函数;并写出函数的定义域.
的函数;并写出函数的定义域.
(ii)设AC=x(km),将y表示成x的函数;并写出函数的定义域.
(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小?
某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20 km,BC=10 km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为y km.
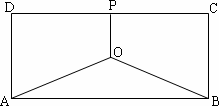
(Ⅰ)按下列要求写出函数关系式:
①设∠BAO=![]() (rad),将y表示成
(rad),将y表示成![]() 的函数关系式;
的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
(Ⅱ)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com