练习册

  • 练习册
  • 试题
    3．关于用二分法求函数的零点近似值的步骤须注意的问题: (1)第一步中要使:①区间长度尽量小,②的值比较容易计算且 , (2)根据函数的零点与相应方程根的关系.求函数的零点与求相应方程根是等价的.对于求方程的根.可以构造函数.函数的零点即方程的根. ★热点考点题型探析 考点1 零点的求法及零点的个数 题型1:求函数的零点. [例1] 求函数的零点. [解题思路]求函数的零点就是求方程的根 [解析]令 .∴ ∴.∴ 即函数的零点为-1.1.2. [名师指引] 函数的零点不是点.而是函数函数的图像与x轴交点的横坐标.即零点是一个实数. 题型2:确定函数零点的个数. [例2] 求函数f(x)=lnx+2x -6的零点个数. [解题思路]求函数f(x)=lnx+2x -6的零点个数就是求方程lnx+2x -6=0的解的个数 [解析]方法一:易证f(x)= lnx+2x -6在定义域上连续单调递增. 又有.所以函数f(x)= lnx+2x -6只有一个零点. 方法二:求函数f(x)=lnx+2x -6的零点个数即是求方程lnx+2x -6=0的解的个数 即求的交点的个数.画图可知只有一个. [名师指引]求函数的零点是高考的热点.有两种常用方法: ①求方程的实数根, ②对于不能用求根公式的方程.可以将它与函数的图像联系起来.并利用函数的性质找出零点． 题型3:由函数的零点特征确定参数的取值范围 [例3] 已知a是实数,函数,如果函数在区间上有零点.求a的取值范围. [解题思路]要求参数a的取值范围.就要从函数在区间上有零点寻找关于参数a的不等式(组).但由于涉及到a作为的系数.故要对a进行讨论 [解析] 若 , ,显然在上没有零点, 所以 . 令 , 解得 ①当 时, 恰有一个零点在上; ②当.即时.在 上也恰有一个零点. ③当在上有两个零点时, 则 或 解得或 综上所求实数的取值范围是 或 . [名师指引]①二次函数.一元二次方程和一元二次不等式是一个有机的整体.也是高考热点.要深刻理解它们相互之间的关系.能用函数思想来研究方程和不等式.便是抓住了关键. ②二次函数f(x)=ax2+bx+c的图像形状.对称轴.顶点坐标.开口方向等是处理二次函数问题的重要依据. [新题导练] 【查看更多】

     

    题目列表(包括答案和解析)

     已知函数。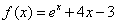

       （Ⅰ）求证函数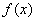在区间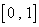上存在唯一的零点，并用二分法求函数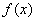零点的近似值（误差不超过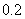）；（参考数据，，，）；

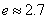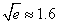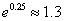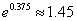       （Ⅱ）当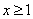时，若关于的不等式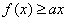恒成立，试求实数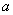的取值范围．

     

     

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    ①函数y=f（-x+2）与y=f（x-2）的图象关于y轴对称；
    ②用二分法求函数f（x）=lnx+x-2在（1，2）上零点的近似值，要求精确度0.1，则至少需要五次对对应区间中点的函数值的计算；
    ③函数f（x）（其中f（x）恒不等于0）满足 f（x）=f（x+1）f（x-1），则f（2013）f（0）=1；
    ④若f（1-x）=-f（x+1），则函数y=f（x-1）的图象关于点（2，0）对称．
    其中正确命题的序号是（　　）

    查看答案和解析>>

    ①函数y=f（-x+2）与y=f（x-2）的图象关于y轴对称；
    ②用二分法求函数f（x）=lnx+x-2在（1，2）上零点的近似值，要求精确度0.1，则至少需要五次对对应区间中点的函数值的计算；
    ③函数f（x）（其中f（x）恒不等于0）满足 f（x）=f（x+1）f（x-1），则f（2013）f（0）=1；
    ④若f（1-x）=-f（x+1），则函数y=f（x-1）的图象关于点（2，0）对称．
    其中正确命题的序号是（　　）
    A．①③④B．②③④C．①②D．③④

    查看答案和解析>>

    ①函数y=f（-x+2）与y=f（x-2）的图象关于y轴对称；
    ②用二分法求函数f（x）=lnx+x-2在（1，2）上零点的近似值，要求精确度0.1，则至少需要五次对对应区间中点的函数值的计算；
    ③函数f（x）（其中f（x）恒不等于0）满足 f（x）=f（x+1）f（x-1），则f（2013）f（0）=1；
    ④若f（1-x）=-f（x+1），则函数y=f（x-1）的图象关于点（2，0）对称．
    其中正确命题的序号是（ ）
    A．①③④
    B．②③④
    C．①②
    D．③④

    查看答案和解析>>

    下列关于二分法的叙述，正确的是

    [　　]

    A．用二分法可以求所有函数的零点的近似值

    B．用二分法求方程近似解时，可以精确到小数点后任一数字

    C．二分法无规律可循，无法在计算机上进行

    D．二分法只用于求方程的近似解

    查看答案和解析>>


    同步练习册答案