
题目列表(包括答案和解析)
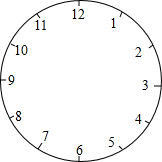 钟面数字问题
钟面数字问题 钟面数字问题
钟面数字问题| ± | 0.03 0.02 |
| ± | 0.03 0.02 |
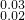 时,?表示直径,单位是毫米(mm).这样标注表示零件直径的标准尺寸是30mm,实际产品的直径最大可以是(30+0.03)mm,最小可以是(30-0.02)mm,在这个范围内的产品都是合格的.如果生产了一个零件的直径是29.97mm,它合格吗?这里的
时,?表示直径,单位是毫米(mm).这样标注表示零件直径的标准尺寸是30mm,实际产品的直径最大可以是(30+0.03)mm,最小可以是(30-0.02)mm,在这个范围内的产品都是合格的.如果生产了一个零件的直径是29.97mm,它合格吗?这里的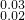 给出了允许误差的大小.允许误差一般用正负数的形式写出.
给出了允许误差的大小.允许误差一般用正负数的形式写出.| ± | 0.030.02 |
| ± | 0.030.02 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com