
题目列表(包括答案和解析)
5.(2005年杭州市)已知一次函数y=kx-k,若y随x的增大而减小,则该函数的图像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第二、三、四象限 D.第一、三、四象限
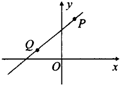
4.如图,直线y=kx+b与x轴交于点(-4,0),则y>0时,x的取值范围是( )
A.x>-4 B.x>0 C.x<-4 D.x<0
3.已知两个一次函数y1=-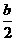 x-4和y2=-
x-4和y2=-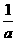 x+
x+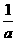 的图象重合,则一次函数y=ax+b的图象所经过的象限为( )
的图象重合,则一次函数y=ax+b的图象所经过的象限为( )
A.第一、二、三象限 B.第二、三、四象限
C.第一、三、四象限 D.第一、二、四象限
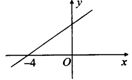
2.如图,一次函数y=kx+b的图象经过A、B两点,则kx+b>0的解集是( )
A.x>0 B.x>2 C.x>-3 D.-3<x<2
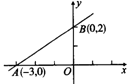
(第2题) (第4题) (第7题)
1.下列各点中,在函数y=2x-7的图象上的是( )
A.(2,3) B.(3,1) C.(0,-7) D.(-1,9)
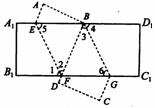
26.如图,矩形A1BlC1D1沿EF折叠,使B1点落在A1D1边上的B处;沿BG折叠,使D1点落在D处且BD过F点.
(1)求证:四边形BEFG是平行四边形;
(2)连结B1B;判断△B1BG的形状,并写出判断过程.
25.取一张矩形的纸片进行折叠,具体操作过程如下:
第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B`,得Rt△AB`E,如图(2);
第三步:沿EB`线折叠得折痕EF,如图(3).
利用展开图(4)探究:
⑴△AEF是什么三角形?
⑵对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
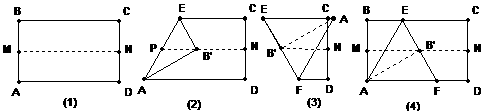
24.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
⑴请根据下列图形,填写表中空格:

|
正多边形边数 |
3 |
4 |
5 |
6 |
… |
n |
|
正多边形每个内角的度数 |
60° |
90° |
108° |
120° |
… |
|
⑵如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
⑶从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
23.⑴四年一度的国际数学家大会于2002年8月20日在北京召开.大会会标如图甲.它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5.求中间小正方形的面积.
⑵现有一张长为6.5cm、宽为2cm的纸片,如图,请你将它分割成6块,再拼合成一个正方形.(要求:先在图乙中画出分割线,再画出拼成的正方形并标明相应数据)
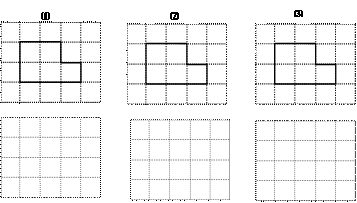
22.现有一块形如母子正方形的板材,木工师傅想先把它分割成几块,然后适当拼接,制成某种特殊形状的板面(要求板材不能有剩余,拼接时不重叠、无空隙),请你按下列要求,帮助木工师傅分别设计一种方案:
⑴板面形状为非正方形的中心对称图形;⑵板面形状为等腰梯形;⑶板面形状为正方形.
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面拼接后的图形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com