7．要了解某市初中毕业会考的数学成绩情况，从中抽查了1000名学生的数学成绩，样本是指………………………………………………………………………………(　　 )

(A)此城市所有参加毕业会考的学生

(B)此城市所有参加毕业会考的学生的数学成绩

(C)被抽查的1 000名学生

(D)被抽查的1 000名学生的数学成绩

[答案]D．

[点评]本题考查样本的意义与识别．

6．在对100个数据进行整理的频率分布表中，各组的频数之和等于________，各组的频率之和等于________．

[答案]100，1．

[点评]本题考查频率分布表中频数、频率的规律．解题时要注意分清频数、频率的意义．

5．已知一个样本含20个数据：

68　 69　 70　 66　 68　 65　 64　 65　 69　 62

　 67　 66　 65　 67　 63　 65　 64　 61　 65　 66．

在列频率分布表时，如果取组距为2，那么应分________组，64.5-66.5这一小组的频率为________，上述样本的容量是____________．

[提示]将一组数据分组时应注意什么？

[答案]5，0.4，20．

[点评]本题考查频率分布中的分组方法及频率计算方法．因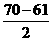＝4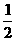，故应分5组，在64.5-66.5之间有8个数据，则＝0.4，即这小组的频率为0.4．

4．数据2，－1，0，－3，－2，3，1的样本标准差为_____________．

[提示]这组数据的方差怎么求？它的标准差与方差有什么关系？

[答案]2．

[点评]本题考查方差、标准差的求法，由

s²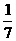＝［2²+(－1)²+0²+(－3)²+(－2)²+3²+1²－7×0］＝4，

故　 s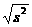＝＝2．

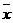或由＝0知，

s ²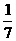＝[2²+(－1)²+0²+(－3)²+(－2)²+3²+1²]＝4，

故　 s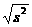＝＝2．

3．在数据－1，0，4，5，8中插入一个数x，使这组数据的中位数为3，则x＝_______．

[提示]插入一个数据后共有几个数据？此时中位数应如何求得？

[答案]2．

[点评]本题考查中位数意义的灵活运用．因为加一个数据后有六个数，故中位数应为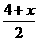，即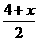＝3，所以x＝2．

2．n个数据的和为56，平均数为8，则n＝__________．

[提示]平均数＝．

[答案]7．

[点评]本题考查平均数的意义．

1．某班的5位同学在向“救助贫困学生”捐款活动中，捐款数如下(单位：元)：8，3，8，2，4，那么这组数据的众数是_______，中位数是_________，平均数是_______．

[答案]8，4，5．

[点评]本题考查众数、中位数、平均数的求法，因8出现两次，故众数为8；把数据按2，3，4，8，8排列，中位数即第三个数4；平均数为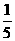(8+3+8+2+4)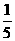＝×25＝5．

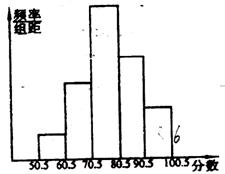
25．某班50名学生期末考试数学成绩(单位：分)的频率分布直方图如图所示，其中学生的成绩均为整数。

⑴成绩在50.5分~60.5分段的人数与90.5分~100.5分段的人数相等；

⑵从左到右数，第四小组的频率是0.03；

⑶成绩在80.5分以上的学生有20人；

⑷本次考试，成绩的中位数在第三小组。

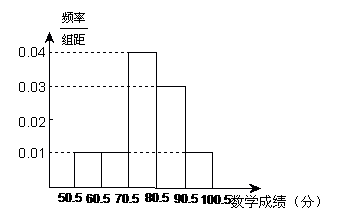
24．某中学初三·三班在上期期末考试中，将学生的成绩进行整理后分成五组，绘成频率颁布直方图(如图)，图中从左到右各小组的小长方形的高的比是1∶3∶6∶4∶2,最右边一组的频数是6。结合频率颁布直方图提供的信息，解答下列问题：(1)该班共有多少名同学参加期末考试？(2)成绩落在哪组数据范围内的人数最多？是多少？(3)求成绩在60分以上(不含60分)的学生占全班总人数的百分率。

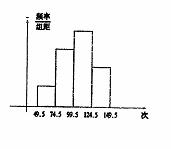
23．为了解小学生的体能情况，抽取某学校一个年级的部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图，如图7，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一个小组的频数为5：

(1)求第四小组的频率。

(2)问参加测试的学生数是多少？

(3)若次数在75以上(含75次)者为达标，试估计该年级测试的达标率是多少？

(4)问这次测试中，学生跳绳的次数为中位数落在哪个小组内？并说明理由。