
题目列表(包括答案和解析)
3.理解自变量的取值范围和函数值的意义,会用描点法画出函数的图象.
内容分析
2.理解常量和变量的意义,了解函数的一般概念,会用解析法表示简单函数;
1.了解平面直角坐标系的有关概念,会画直角坐标系,能由点的坐标系确定点的位置,由点的位置确定点的坐标;
7、小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大。
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连结OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=300,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)第(1)题中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
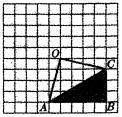
6、如图,在网格中有一个四边形图案。
(1)请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论。
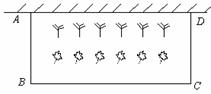
5、某市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的BC边长为x(m),花园的面积为y(m2).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200 m2吗?若能,求出此时x的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x取何值时,花园的面积最大?最大面积为多少?
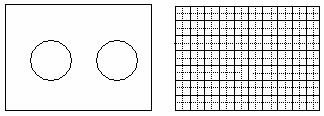
4、有一长方形的餐厅,长10m,宽7m,现只摆放两套同样大小的圆桌和椅子,一套圆桌和椅子占据的地面部分可看成半径为1.5m的圆形(如图所示).在保证通道最狭窄处的宽度不小于0.5m的前提下,问此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢?请在摆放三套或四套的两种方案中选取一种,在右下方14×20方格纸内画出设计示意图.(提示:①画出的圆应符合比例要求;②为了保证示意图的清晰,请你在有把握后才将设计方案正式画在方格纸上)
3、台球是一项高雅的体育运动.其中包含了许多物理学、几何学知识。图①是一个台球桌,目标球F与本球E之间有一个G球阻挡
(1)击球者想通过击打E球先撞击球台的AB边.经过一次反弹后再撞击F球。他应将E球打到AB边上的哪一点?请在图①中用尺规作出这一点H.并作出E球的运行路线;(不写画法.保留作图痕迹)

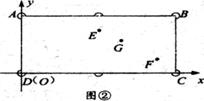 (2)如图②.现以D为原点,建立直角坐标系,记A(O,4).C(8,0).E(4,3),F(7,1),求E球接刚才方式运行到F球的路线长度.(忽略球的太小)
(2)如图②.现以D为原点,建立直角坐标系,记A(O,4).C(8,0).E(4,3),F(7,1),求E球接刚才方式运行到F球的路线长度.(忽略球的太小)
图①
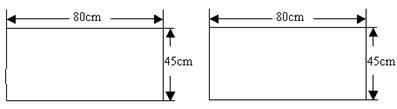
2、蓝天希望学校正准备建一个多媒体教室,计划做长120cm,宽30cm的长条形桌面。现只有长80cm,宽45cm的木板,请你为该校设计不同的拼接方案,使拼出来的桌面符合要求。(只要求画出裁剪、拼接图形,并标上尺寸,设计出一种得5分,设计出两种再加1分)
1、如图①,将矩形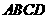 沿着对角线
沿着对角线 分割,得到
分割,得到 和
和 ,将
,将 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转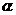 度,使
度,使 三点在同一直线上,得到图②,再把图②中的
三点在同一直线上,得到图②,再把图②中的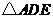 沿着
沿着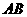 方向平移
方向平移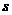 格,使点
格,使点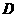 与点
与点 重合,得到图③,设
重合,得到图③,设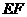 与
与 相交于点
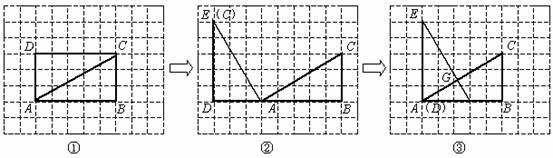
相交于点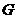 .
.
请解答以下问题:
(1)上述过程中,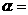 度,
度,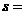 格;
格;
(2)在图③中,除了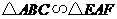 以外,还能找出 对相似三角形;
以外,还能找出 对相似三角形;
(3)请写一对你在图③中找出的相似三角形,并加以证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com