
题目列表(包括答案和解析)
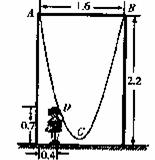
6.如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状.
(1) (2)
??(1)一身高0.7米的小孩站在离立柱0.4米处,其头部刚好触上绳子,求绳子最低点到地面的距离;
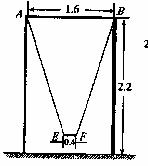
??(2)为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳长正好各为2米,木板与地面平行.求这时木板到地面的距离(供选用数据: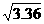 ≈1.8,
≈1.8,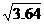 ≈1.9,
≈1.9,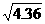 ≈2.1)
≈2.1)
5.某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
|
每件销售价(元) |
50 |
60 |
70 |
75 |
80 |
85 |
… |
|
每天售出件数 |
300 |
240 |
180 |
150 |
120 |
90 |
… |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察这些统计数据,找出每天售出件数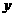 与每件售价
与每件售价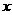 (元)之间的函数关系,并写出该函数关系式.
(元)之间的函数关系,并写出该函数关系式.
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.
求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
4.已知函数y=x2+bx-1的图象经过点(3,2)
(1) 求这个函数的解析式;
(2) 画出它的图象,并指出图象的顶点坐标;
(3) 当x>0时,求使y≥2的x的取值范围.
3.看图,解答下列问题.
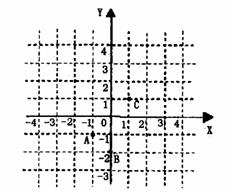
(1)求经过A、B、C三点的抛物线解析式;
(2)通过配方,求该抛物线的顶点坐标和对称轴;
(3)用平滑曲线连结各点,画出该函数图象.
1已知二次函数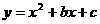 的图像经过A(0,1),B(2,-1)两点.
(1)求b和c的值;
(2)试判断点P(-1,2)是否在此函数图像上?
的图像经过A(0,1),B(2,-1)两点.
(1)求b和c的值;
(2)试判断点P(-1,2)是否在此函数图像上?
2.已知一次函数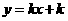 的图象与反比例函数
的图象与反比例函数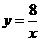 的图象交于点P(4,n).
的图象交于点P(4,n).
(1)求n的值.(2)求一次函数的解析式.
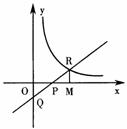
10.如图,直线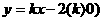 与双曲线
与双曲线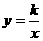 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
9. 二次函数
二次函数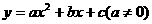 的图像与x轴交点横坐标为-2,b,图像与y轴交点到圆点距离为3,则该二次函数的解析式为___________;
的图像与x轴交点横坐标为-2,b,图像与y轴交点到圆点距离为3,则该二次函数的解析式为___________;
8.某学生在体育测试时推铅球,千秋所经过的路线是二次函数图像的一部分,如果这名学生出手处为A(0,2),铅球路线最高处为B(6,5),则该学生将铅球推出的距离是________;
7.某商场销售一批名牌衬衫,平均每天可售出20件,每件可 盈利40元.为了扩大销售量,增加盈利,采取了降价措施,经调查发现如果每件计划降价1元,那么商场平均每天可多售出2件.若商场平均每天要赢利1200元,则每件衬衫应降价__________;
6.抛物线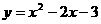 向左平移5各单位,再向下平移2个单位,所得抛物线的解析式为___________;
向左平移5各单位,再向下平移2个单位,所得抛物线的解析式为___________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com