
题目列表(包括答案和解析)
6、已知扇形的圆心角为150°,它所对弧长为20πcm,则扇形的半径是 cm,扇形的面积是 cm2;
5、圆锥底面半径为6cm,母线长为10cm,则它的侧面展开图圆心角等于 度,表面积为 ;
4、正六边形的内切圆半径与外接圆半径的比等于_________.
3、边长为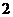 的正方形的外接圆的面积等于________.
的正方形的外接圆的面积等于________.
2、正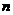 边形的中心角的度数是_______.
边形的中心角的度数是_______.
1、在一个圆中,如果 的弧长是
的弧长是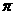 ,那么这个圆的半径
,那么这个圆的半径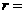 _________.
_________.
4.弓形的面积
(1)弓形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做 。
(2)弓形的周长=
(3)弓形的面积
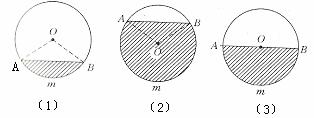
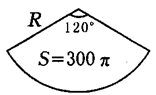
当弓形所含的弧是劣弧时,如图1所示,s弓形=
当弓形所含的弧是优弧时,如图2所示,s弓形
当弓形所含的弧是半圆时,如图3所示,s弓形
[例题解析]
例:已知扇形的圆心角为120°,面积为300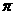 cm2.
cm2.
(1)求扇形的弧长;
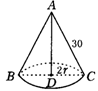
(2)若将此扇形卷成一个圆锥,则这个圆锥的轴截面面积为多少?
 解析:(1)由S扇形=
解析:(1)由S扇形=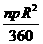 求出R,再代入L=
求出R,再代入L=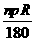 求得.(2)若将此扇形卷成一个圆锥,扇形的弧长就是圆锥底面圆的周长,就可求圆的半径,其截面是一个以底是直径,圆锥母线为腰的等腰三角形.解答如下:(1)如图所示:∵300
求得.(2)若将此扇形卷成一个圆锥,扇形的弧长就是圆锥底面圆的周长,就可求圆的半径,其截面是一个以底是直径,圆锥母线为腰的等腰三角形.解答如下:(1)如图所示:∵300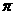 =
=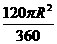 ; ∴R=30; ∴弧长L=
; ∴R=30; ∴弧长L=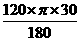 =20
=20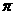 (cm)(2)如右图所示:∵20
(cm)(2)如右图所示:∵20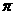 =20
=20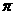 r; ∴r=10,R=30。
AD=
r; ∴r=10,R=30。
AD=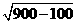 =20
=20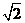 ∴S轴截面=
∴S轴截面=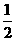 ×BC×AD=
×BC×AD=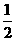 ×2×10×20
×2×10×20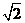 =200
=200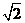 (cm2);因此,扇形的弧长是20
(cm2);因此,扇形的弧长是20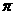 cm卷成圆锥的轴截面是200
cm卷成圆锥的轴截面是200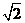 cm2.
cm2.
反思:圆锥、扇形、圆之间的换算是中考中的热点、常考点,需同学们理清平面与立体之间的变换和实质,熟悉公式并能利用题目中的数据代替公式中的量来解题。
[实弹射击]
3. 圆锥的侧面积与表面积
(1)如图1: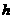 为圆锥的 ,
为圆锥的 ,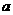 为圆锥的 ,
为圆锥的 , 为圆锥的 ,由勾股定理可得:
为圆锥的 ,由勾股定理可得: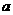 、
、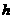 、
、 之间的关系为:
之间的关系为:
(2)如图2:圆锥的侧面展开后是一个 :圆锥的母线是扇形的 ,而扇形的弧长恰好是圆锥底面的
;故:圆锥的侧面积就是圆锥的侧面展开后的扇形的面积,即是
;圆锥的表面积=
(圆周率用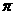 表示即可)
表示即可)
2. 扇形面积计算:
方法一:如果已知扇形圆心角为n,半径为R,那么扇形面积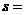
方法二:如果已知扇形弧长为l,半径为R, 那么扇形面积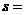
1. 弧长公式:在半径为R的圆中,n°圆心角所对的弧长的计算公式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com