
题目列表(包括答案和解析)
8.设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l
的斜率的取值范围是 ( )
A.[-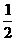 ,
,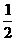 ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
7.椭圆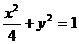 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点
为P,则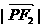 = ( )
= ( )
A.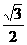 B.
B.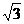 C.
C.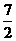 D.4
D.4
5.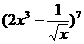 的展开式中常数项是 ( )
的展开式中常数项是 ( )
A.14 B.-14 C.42 D.-42
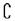
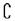
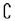 6.设A、B、I均为非空集合,且满足A
6.设A、B、I均为非空集合,且满足A B
B  I,则下列各式中错误的是 ( )
I,则下列各式中错误的是 ( )
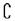
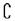
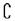
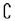 A.( I A)∪B=I B.( I A)∪( I B)=I
A.( I A)∪B=I B.( I A)∪( I B)=I
C.A∩( I B)=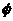 D.( I A)∪( I B)= I B
D.( I A)∪( I B)= I B
4.函数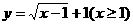 的反函数是 ( )
的反函数是 ( )
A.y=x2-2x+2(x<1) B.y=x2-2x+2(x≥1)
C.y=x2-2x (x<1) D.y=x2-2x (x≥1)
3.已知a、b均为单位向量,它们的夹角为60°,那么|a+3b|= ( )
A.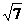 B.
B.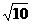 C.
C.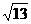 D.4
D.4
2.已知函数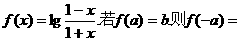 ( )
( )
A.b B.-b C.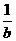 D.-
D.-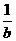
1.(1-i)2·i= ( )
A.2-2i B.2+2i C.-2 D.2
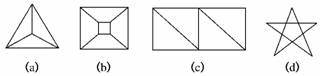
13.下面的(a)、(b)、(c)、(d)为四个平面图.
(1)数一数,每个平面图各有多少个顶点?多少条边?它们分别围成了多少个区域?请将结果填入下表(按填好的例子做).
|
|
顶点数 |
边数 |
区域数 |
|
(a) |
4 |
6 |
3 |
|
(b) |
|
|
|
|
(c) |
|
|
|
|
(d) |
|
|
|
(2)观察上表,推断一个平面图的顶点数、边数、区域数之间有什么关系?
(3)现已知某个平面图有2008个顶点,且围成了2008个区域,试根据以上关系确定这个平面图的边数.
解:(1)填表如下:
|
|
顶点数 |
边数 |
区域数 |
|
(a) |
4 |
6 |
3 |
|
(b) |
8 |
12 |
5 |
|
(c) |
6 |
9 |
4 |
|
(d) |
10 |
15 |
6 |
(2)由上表可以看出,所给的四个平面图的顶点数、边数及区域数之间有下述关系:
4+3-6=1
8+5-12=1
6+4-9=1
10+6-15=1
由此,我们可以推断:任何平面图的顶点数、边数及区域数之间,都有下述关系:
顶点数+区域数-边数=1.
(3)由(2)中所得出的关系,可知所求平面图的边数为:
边数=顶点数+区域数-1=2008+2008-1=4015
12.在△ABC中,AB⊥AC,AD⊥BC于D,求证:=+,那么在四面体ABCD中,类比上述结论,你能得到怎样的猜想,并说明理由.
解:如图(1)所示,由射影定理AD2=BD·DC,AB2=BD·BC,AC2=BC·DC,
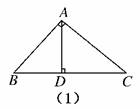
∴=
==.
又BC2=AB2+AC2,
∴==+.
所以=+.
猜想:类比AB⊥AC,AD⊥BC猜想
四面体ABCD中,AB、AC、AD两两垂直,AE⊥平面BCD.则=++.
如图(2),连接BE交CD于F,连接AF.
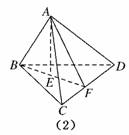
∵AB⊥AC,AB⊥AD,
∴AB⊥平面ACD.
而AF⊂面ACD,
∴AB⊥AF.
在Rt△ABF中,
AE⊥BF,
∴=+.
在Rt△ACD中,AF⊥CD,
∴=+.
∴=++,故猜想正确.
11.观察下列等式:
①sin210°+cos240°+sin10°cos40°=;
②sin26°+cos236°+sin6°cos36°=.
由上面两题的结构规律,你是否能提出一个猜想?并证明你的猜想.
解:由①②可看出,两角差为30°,则它们的相关形式的函数运算式的值均为.
猜想:若β-α=30°,则β=30°+α,
sin2α+cos2β+sinαcosβ=,
也可直接写成sin2α+cos2(α+30°)+sinαcos(α+30°)=.
下面进行证明:
左边=++sinαcos(α+30°)
=++sinα(cosα·cos30°-sinαsin30°)
=-cos2α++cos2α-sin2α+sin2α-
==右边.
故sin2α+cos2(α+30°)+sinαcos(α+30°)=.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com