
题目列表(包括答案和解析)
22.(本小题满分14分)
已知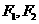 分别是双曲线
分别是双曲线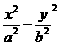 =l(a>0,b>0)的左、右焦点,P为双曲线上的一点,若
=l(a>0,b>0)的左、右焦点,P为双曲线上的一点,若 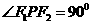 ,且
,且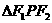 的三边长成等差数列.又一椭圆的中心在原点,短轴的一个端点到其右焦点的距离为
的三边长成等差数列.又一椭圆的中心在原点,短轴的一个端点到其右焦点的距离为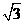 ,双曲线与该椭圆离心率之积为
,双曲线与该椭圆离心率之积为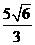 。
。
(I)求椭圆的方程;
(Ⅱ)设直线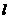 与椭圆交于A,B两点,坐标原点O到直线l的距离为
与椭圆交于A,B两点,坐标原点O到直线l的距离为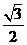 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
21.(本小题满分12分)
甲方是一农场,乙方是一工厂,乙方生产须占用甲方的资源,甲方每年向乙方索赔以弥补经济损失并获得一定的净收入乙方在赔付甲方前,年纯收入P(元)与年产量t(吨)满足函数关系P=2000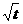 ;若乙方每生产一吨产品必须赔付甲方s(元)(以下称s为赔付价格),则其年利润为Q(元).
;若乙方每生产一吨产品必须赔付甲方s(元)(以下称s为赔付价格),则其年利润为Q(元).
(I)求乙方的年利润Q(元)关于年产量t(吨)的函数表达式,并求出当年利润Q(元)最大时的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失为y=0.002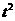 (元),在乙方按照获得最大年利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?(净收入=获赔金额-经济损失)
(元),在乙方按照获得最大年利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?(净收入=获赔金额-经济损失)
20.(本小题满分12分)
如图,三棱台ABC-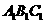 中,
中,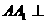 平面ABC,
平面ABC,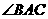 =
=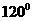 ,AB=AC=A
,AB=AC=A =2
=2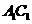 , D为BC的中点.
, D为BC的中点.
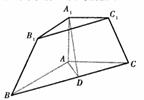 (I)证明:平面A1AD⊥平面BCC1B1;
(I)证明:平面A1AD⊥平面BCC1B1;
(Ⅱ)求二面角A-CC1-B的余弦值.
19.(本小题满分12分)
已知数列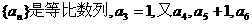 成等差数列,数列
成等差数列,数列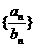 的前
的前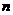 项和
项和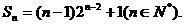
(I)求数列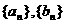 的通项公式;
的通项公式;
(Ⅱ)设数列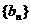 的前n项和为
的前n项和为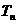 ,若如
,若如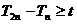 对一切正整数n都成立,求实数t的取值范围.
对一切正整数n都成立,求实数t的取值范围.
18.(本小题满分12分)
在A、B两个口袋中均有2个红球和2个白球,先从A袋中任取2个球转放到B袋中,再从B袋中任取l个球转放到A袋中,结果A袋中恰有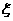 个红球.
个红球.
(I)求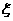 =2时的概率;
=2时的概率;
(II)求随机变量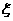 的分布列及期望.
的分布列及期望.
17.(本小题满分12分)
已知函数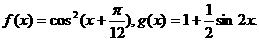
(I)设x=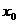 是函数
是函数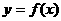 图象的一条对称轴,求
图象的一条对称轴,求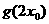 的值;
的值;
(Ⅱ)求函数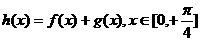 的值域.
的值域.
16.已知点P在直线卅x+2y-1=0上,点Q在直线x+2y+3=0上,PQ中点为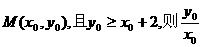 的取值范围为
的取值范围为
15.如图,连接函数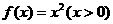 上任意两点A(a,
上任意两点A(a,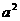 )
)
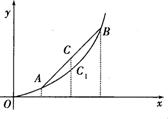
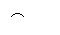 B(b,
B(b,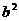 ),线段AB必在AB上方,设点C是线段AB的中点,
),线段AB必在AB上方,设点C是线段AB的中点,
则由图中C在 ,的上方可得不等式:
,的上方可得不等式: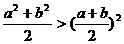 .
.
请分析函数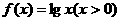 的图象,类比上述不等式可以得
的图象,类比上述不等式可以得
到 .
14.已知函数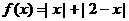 ,若函数
,若函数
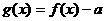 的零点个数不为0,
的零点个数不为0,
则a的最小值为 .
把正确答案填在答题纸给定的横线上.
13.运行如图所示的程序框图,其输出结果为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com