
题目列表(包括答案和解析)
2. 与向量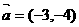 同方向的单位向量是
同方向的单位向量是
1. 已知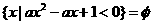 ,则实数a的取值范围是
,则实数a的取值范围是
4.(1998年全国)sin600°的值是( )。
A、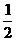 B、
B、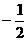 C、
C、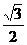 D、
D、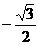
解:sin600°=sin(360°+240°)=sin240°
=sin(180°+60°)=-sin60°
=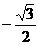
∴应选D。
3.(1998年全国)已知点P(sina-cosa,tga)在第一象限,则在[0,2p]内a的取值范围是( )
A、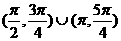 B、
B、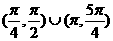
C、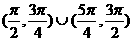 D、
D、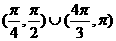
解:由题设,有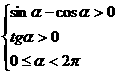
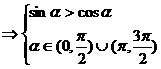
在[0,2p)的范围内,在同一坐标系中作出y=sinx和y=cosx的图像,可在aÎ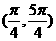 时,sina>cosa。
时,sina>cosa。
∴aÎ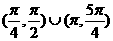
应选B。
2.(2001年全国) 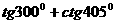 的值为( )。
的值为( )。
A、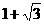 B、
B、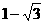 C、
C、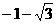 D、
D、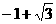
解: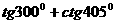
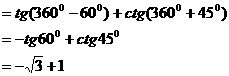
∴ 应选B。
正、余弦函存在着有界性,即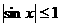 ,
,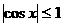 ,在一些数学问题中灵活地加以运用,沟通三角函数与数值间的关系,能大大简化解题过程。
,在一些数学问题中灵活地加以运用,沟通三角函数与数值间的关系,能大大简化解题过程。
例1.若实数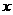 满足
满足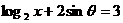 ,求
,求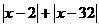 的值。
的值。
解:原方程可化为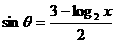 ,
,
因为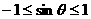 ,所以
,所以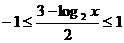 ,
,
所以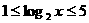 ,所以
,所以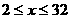
所以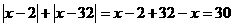 。
。
例2.在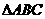 中,
中,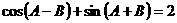 ,试判定三角形的形状。
,试判定三角形的形状。
解:因为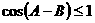 ,
,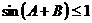 ,又
,又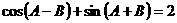 ,
,
所以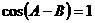 ,
,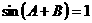
而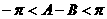 ,
,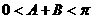 ,
,
于是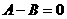 ,
,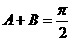
所以,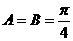 。故
。故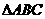 为等腰直角三角形。
为等腰直角三角形。
例3.已知四边形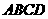 中的角
中的角 、
、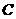 满足
满足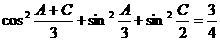
求证: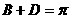
证明:由已知条件有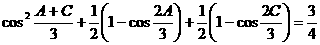
所以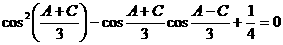
由于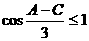 。从而
。从而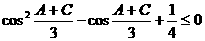
所以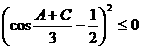 ,但
,但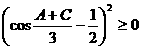 ,
,
所以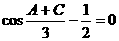 ,
,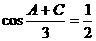 。
。
所以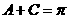 ,故
,故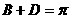 。
。
例4.已知函数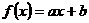 ,
,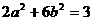 ,求证:对于任意
,求证:对于任意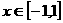 ,有
,有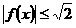 。
。
证明:因为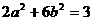 ,所以
,所以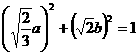 。
。
令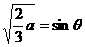 ,
,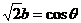 ,则
,则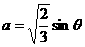 ,
,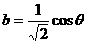
所以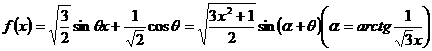
从而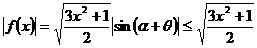
又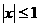 ,故
,故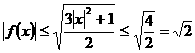
例5.证明: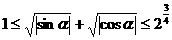 。
。
证明:设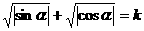 ,则只须证明
,则只须证明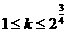 。
。
因为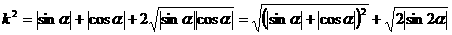
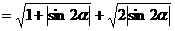
因为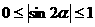 ,所以
,所以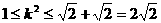 ,
,
从而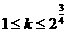 。故
。故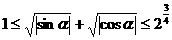 。
。
例6.复数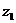 ,
,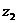 ,
,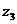 的幅角分别为
的幅角分别为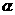 、
、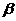 、
、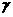 ,
,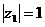 ,
,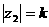 ,
,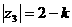 ,且
,且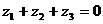 ,问
,问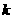 为何值时,
为何值时,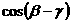 分别取得最大值和最小值,并求出最大值和最小值。
分别取得最大值和最小值,并求出最大值和最小值。
解;因为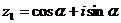 ,
,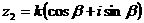 ,
, ,
,
因为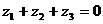 ,
,
所以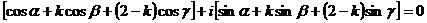 。
。
因而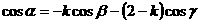 ,
,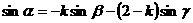 。
。
两式平方相加得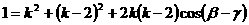
由题设知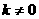 ,
,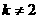 ,
,
所以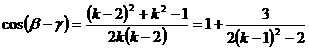 ……(*)
……(*)
因为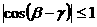 ,所以
,所以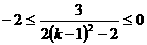 ,
,
解之得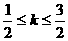 。
。
由(*)知,当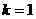 时,
时,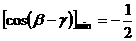 。
。
又由(*)及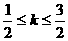 知,当
知,当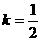 、
、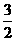 时,
时,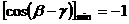 。
。
例7.设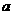 为无理数,求证:函数
为无理数,求证:函数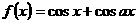 不可能是周期函数。
不可能是周期函数。
证明:假设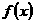 是周期函数,则存在常数
是周期函数,则存在常数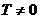 ,使对于任意的
,使对于任意的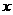 ,
,
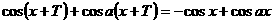 都成立。
都成立。
令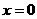 得,
得,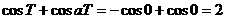
因为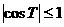 ,
,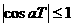 ,所以
,所以
从而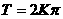 ,
,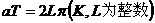
所以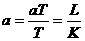 。
。
此时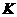 ,
,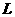 为整数,则
为整数,则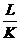 为有理数,但
为有理数,但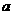 为无理数,这是不可能的,故命题成立。
为无理数,这是不可能的,故命题成立。
1.(2002年全国)在(0,2p)内,使sinx>cosx成立的x取值范围为( )。
A、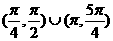 B、
B、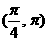
C、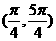 D、
D、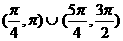
解:在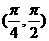 内,sinx>cosx,在
内,sinx>cosx,在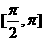 内sinx>cosx;在
内sinx>cosx;在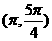 内,sinx>cosx;综上,∴ 应选C。
内,sinx>cosx;综上,∴ 应选C。
10.设aÎ(0, 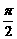 ),
),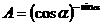 ,
,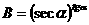 的大小是( )
的大小是( )
A、A>B B、A≥B C、A<B D、A≤B
答案: B B D C D A D C B C
9.化简三角函数式tg(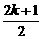 p+
p+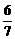 p) (kÎZ), 结果是( )
p) (kÎZ), 结果是( )
A、tg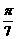 B、ctg
B、ctg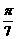 C、ctg
C、ctg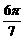 D、-tg
D、-tg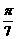
8.如果一弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( )
A、sin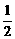 B、
B、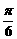 C、
C、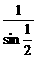 D、2sin
D、2sin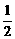
7.若sin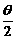 =
=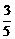 ,cos
,cos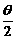 =-
=-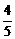 ,则qÎ[0, 2p],终边在( )
,则qÎ[0, 2p],终边在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com