
题目列表(包括答案和解析)
20.(本小题满分12分)
已知椭圆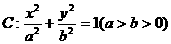 的离心率为
的离心率为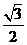 ,过焦点且垂直于长轴的直线被椭圆截得的弦长为
,过焦点且垂直于长轴的直线被椭圆截得的弦长为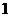 ,过点
,过点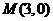 的直线与椭圆
的直线与椭圆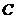 相交于两点
相交于两点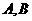 ,
,
(1)求椭圆的方程;
(2)设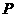 为椭圆上一点,且满足
为椭圆上一点,且满足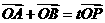 (
( 为坐标原点),当
为坐标原点),当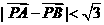 时,求实数
时,求实数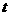 的取值范围
的取值范围
21、解:(1)由题设,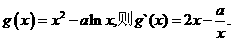 (1分)
(1分)
由已知,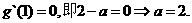 (2分)
(2分)
于是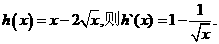 (3分)
(3分)
由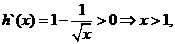 所以
所以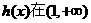 上是增函数,在(0,1)上是减函数。 (4分)
上是增函数,在(0,1)上是减函数。 (4分)
(2)当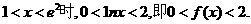 (5分)
(5分)
欲证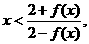 只需证
只需证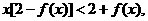 即证
即证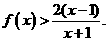 (6分)
(6分)
设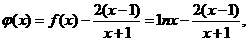
则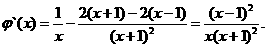
当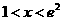 时,
时,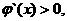 所以
所以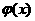 在区间
在区间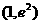 上为增函数。
(7分)
上为增函数。
(7分)
从而当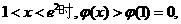 即
即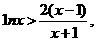 故
故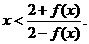 (8分)
(8分)
(3)由题设,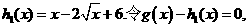
则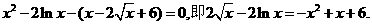 (9分)
(9分)
设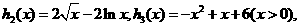
则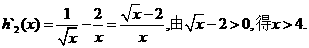
所以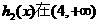 上是增函数,在(0,4)上是减了函数。
(10分)
上是增函数,在(0,4)上是减了函数。
(10分)
 又
又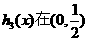 上是增函数,在
上是增函数,在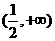 上是减函数。
上是减函数。
因为当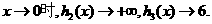
又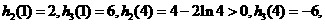
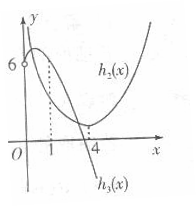
则函数 的大致图象如右:
的大致图象如右:
由图可知,当 两个函数图象有2个交点,故函数
两个函数图象有2个交点,故函数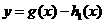 有2个零点。 (13分)
有2个零点。 (13分)
21、(本题13分)给出定义在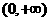 上的三个函数:
上的三个函数: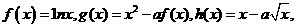 已知
已知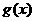 在
在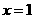 处取得极值。
处取得极值。
(1)确定函数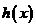 的单调性;
的单调性;
(2)求证:当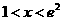 时,恒有
时,恒有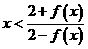 成立;
成立;
(3)把函数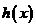 的图象向上平移6个单位长度得到函数
的图象向上平移6个单位长度得到函数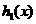 的图象,试确定函数
的图象,试确定函数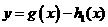 的零点个数,并说明理由。
的零点个数,并说明理由。
20、(1)解:连接PC,由垂径分弦定理知,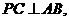 所以点P的轨迹是以线段AC为直径的圆(除去点A)。
所以点P的轨迹是以线段AC为直径的圆(除去点A)。
(2分)
因为点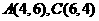 ,则其中点坐标为(5,5),又圆半径
,则其中点坐标为(5,5),又圆半径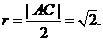
故点P的轨迹方程是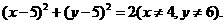 (5分)
(5分)
(2)因为点P、E关于点D(9,0)对称,设点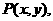 则点
则点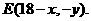 (6分)
(6分)
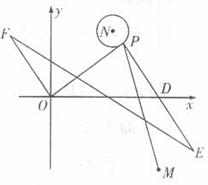 设点
设点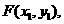 因为线段OF由OP绕原点逆时针旋转90度得到,
因为线段OF由OP绕原点逆时针旋转90度得到,
则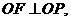 且
且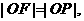 即
即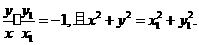
由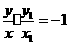 ,得
,得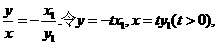
则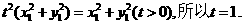 因此点F的坐标为
因此点F的坐标为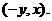
所以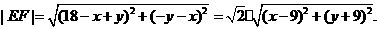
设点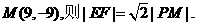 (10分)
(10分)
因为点P为圆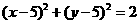 上的点,设圆心为
上的点,设圆心为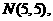
则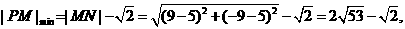
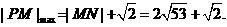 (12分)
(12分)
故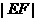 的取值范围是
的取值范围是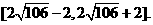 (13分)
(13分)
20、(本题13分)过圆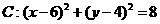 上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点。
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点。
(1)求点P的轨迹方程;
(2)设点P关于点D(9,0)的对称点为E,O为坐标原点,将线段OP绕原点O依逆时针方向旋转90度后,所得线段为OF,求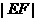 的取值范围。
的取值范围。
19、解:(1)设第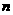 年底该县农村医保基金为
年底该县农村医保基金为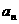 万元,
万元,
则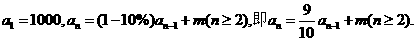 (3分)
(3分)
于是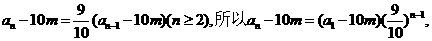
即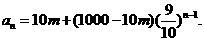 (6分)
(6分)
故第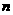 年底该县农村医保基金有
年底该县农村医保基金有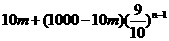 万元。
(7分)
万元。
(7分)
(2)若每年年底的医保基金逐年增加,则数列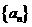 单调递增,
单调递增,
因为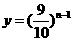 是减函数,则
是减函数,则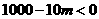 时,即
时,即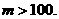 时
(10分)
时
(10分)
又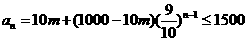 恒成立,则
恒成立,则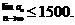
即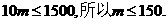 (12分)
(12分)
故每年新增医保基金 的应控制在100万元到150万元之间。
(13分)
的应控制在100万元到150万元之间。
(13分)
19、(本题13分)某县为了贯彻落实党中央国务院关于农村医疗保险(简称“医保”)政策,制定了如下实施方案:2009年底通过农民个人投保和政府财政投入,共集资1000万元作为全县农村医保基金,从2010年起,每年报销农民的医保费都为上一年底医保基金余额的10%,并且每年底县财政再向医保基金注资 万元(
万元( 为正常数)。
为正常数)。
(1)以2009年为第一年,求第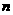 年底该县农村医保基金有多少万元?
年底该县农村医保基金有多少万元?
(2)根据该县农村人口数量和财状况,县政府决定每年年底的医保基金要逐年增加,同时不超过1500万元,求每年新增医保基金 (单位:万元)应控制在什么范围内。
(单位:万元)应控制在什么范围内。
2.新一模
22.解:(Ⅰ)∵OA=[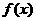 +2
+2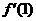 ]OB-
]OB-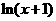 OC,且A、B、C在直线
OC,且A、B、C在直线 上,
上,

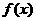 +2
+2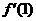 ―
―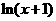 =1, …………(2分)
=1, …………(2分)
 y=
y=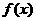 =
=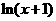 +1-2
+1-2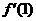 ,
,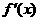 =
=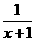 ,于是
,于是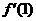 =
=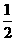 ,
,

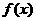 =
=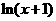 ………(4分)
………(4分)
(Ⅱ)令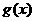 =
=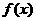 -
-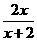 ,由
,由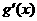 =
=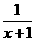 -
-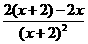 =
=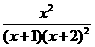 ,
,
以及x>0,知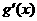 >0,
>0,
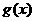 在
在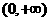 上为增函数,又
上为增函数,又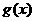 在x=0处右连续,
在x=0处右连续,
 当x>0时,得
当x>0时,得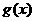 >
>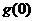 =0,
=0,
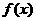 >
>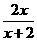 …………(8分)
…………(8分)
(Ⅲ)原不等式等价于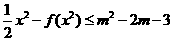 ,
,
令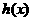 =
=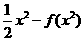 =
=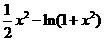 ,则
,则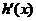 =
=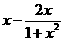 =
=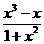 ,(10分)
,(10分)
∵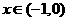 时,
时,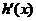 >0,
>0,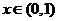 时,
时,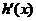 <0,
<0,

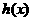 在
在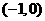 为增函数,在
为增函数,在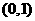 上为减函数,
…………(11分)
上为减函数,
…………(11分)
 当
当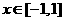 时,
时,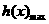 =
= =0,从而依题意有0
=0,从而依题意有0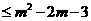 ,
,
解得 ,故m的取值范围是
,故m的取值范围是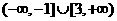 …………(12分)
…………(12分)
22.(本小题满12分)
已知A、B、C是直线l上的三点,O是直线l外一点,向量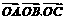 满足
满足
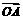 =[f(x)+2f ′(1)]
=[f(x)+2f ′(1)] 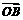 -ln(x+1)
-ln(x+1)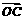
(Ⅰ)求函数y=f(x)的表达式;
(Ⅱ)若x>0,证明:f(x)>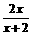 ;
;
(Ⅲ)若不等式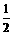 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com