
题目列表(包括答案和解析)
1. 点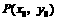 到直线
到直线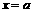 的距离
的距离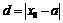 ;点
;点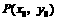 到直线
到直线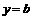 的距离
的距离 ;
;
证明线共点,就是要证明这些直线都过其中两条直线的交点.解决此类问题的一般方法
是:先证其中两条直线交于一点,再证该点也在其他直线上.
 例2 如图2,已知空间四边形
例2 如图2,已知空间四边形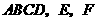 分别是
分别是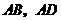 的中点,
的中点,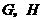 分别是
分别是 上的点,且
上的点,且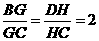 ,求证:
,求证: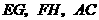 相交于同一点
相交于同一点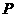 .
.
证明: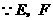 分别是
分别是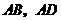 的中点,
的中点,
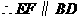 ,且
,且 .
.
又 ,
, ,且
,且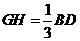 ,
,
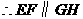 ,且
,且 .
.
 四边形
四边形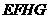 是梯形,其两腰必相交,
是梯形,其两腰必相交,
设两腰 相交于一点
相交于一点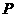 ,
,
 平面
平面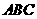 ,
,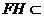 平面
平面 ,
,
 平面
平面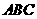 ,
,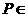 平面
平面 ,
,
又平面 平面
平面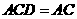 ,
, .
.
故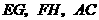 相交于同一点
相交于同一点 .
.
证明点共线,常常采用以下两种方法:①转化为证明这些点是某两个平面的公共点,然后根据公理3证得这些点都在这两个平面的交线上;②证明多点共线问题时,通常是过其中两点作一直线,然后证明其他的点都在这条直线上.
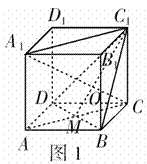 例1 如图1,正方体
例1 如图1,正方体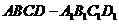 中,
中,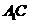 与截面
与截面 关于
关于 点,
点,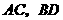 交于
交于 点,求证:
点,求证: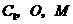 三点共线.
三点共线.
证明: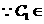 平面
平面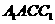 ,且
,且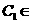 平面
平面 ,
,
 是平面
是平面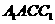 与平面
与平面 的公共点.
的公共点.
又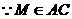 ,
,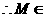 平面
平面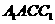 .
.
 ,
,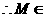 平面
平面 .
.
 也是平面
也是平面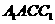 与平面
与平面 的公共点.
的公共点.
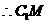 是平面
是平面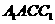 与平面
与平面 的交线.
的交线.
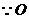 为
为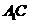 与截面
与截面 的交点,
的交点,
 平面
平面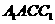 ,
,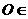 平面
平面 ,即
,即 也是两平面的公共点.
也是两平面的公共点.
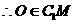 ,即
,即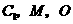 三点共线.
三点共线.
4、一个重要的例题
本例可以作为判定异面直线的定理.
例 过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线.
 如图3,已知
如图3,已知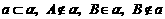 ,
,
求证:直线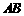 和
和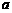 是异面直线.
是异面直线.
证明:假设直线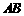 和
和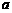 不是异面直线,
不是异面直线,
则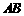 与
与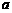 一定共面,设为
一定共面,设为 ,则
,则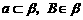 .
.
因为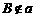 所以由公理3的推论1:经过一条直线及其直线外的一
所以由公理3的推论1:经过一条直线及其直线外的一
点,有且只有一个平面,可知,直线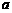 与点
与点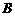 确定一个平面,
确定一个平面,
即为 ,则
,则 与
与 重合.
重合.
所以 ,这与
,这与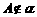 矛盾.
矛盾.
所以直线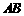 与
与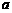 是异面直线.
是异面直线.
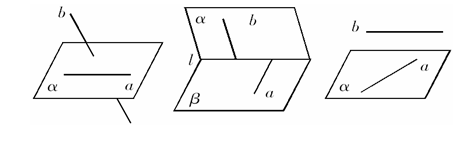
3、异面直线的画法
画异面直线时,为了充分显示它们既不平行又不相交的特点,
即不共面的特点,常常要以辅助平面作为衬托,以增强其直观性,通常画成以下几种情形:
2、不能把异面直线误解为分别在不同平面内的两条直线.
如图1,在长方体 中,
中,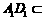 平面
平面 ,
,
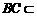 平面
平面 ,但
,但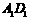 与
与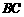 的位置关系是平行,而不是异面.
的位置关系是平行,而不是异面.
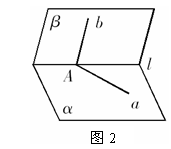 又如图2,平面
又如图2,平面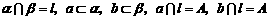 ,
,
由于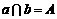 ,所以
,所以 不是异面直线.
不是异面直线.
也就是说,在两个不同平面内的直线,它们既可以是平行直线,
也可以是相交直线.
6.平面几何中的结论或者定理在立体几何中不一定成立.在使用过程中应注意加以甄别,看哪些成立,哪些不成立.
5.对于异面直线,它们是既不平行也不相交的,即不存在或者说找不到使它们共面的平面.这一点希望同学们在学习中认真体会.
4.异面直线的概念是研究直线和直线、直线和平面、平面和平面各种位置关系的基础,要注意区分定义中“不同在任何一个平面内”和“不在同一个平面内”的区别,这是正确理解异面直线概念的关键.
3.公理4是立体几何中平行关系过渡的重要原理,因为它是判断两条直线平行的重要方法,即寻找第三条直线分别与前两条平行,并且这种平行关系的传递不受直线条数的限制.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com