
题目列表(包括答案和解析)
已知定点![]() ,动点B是圆F:
,动点B是圆F:![]() (F为圆心)上一点,线段AB的垂直平分线交BF与P。
(F为圆心)上一点,线段AB的垂直平分线交BF与P。
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)直线![]() 交P点的轨迹于M、N两点,若P点的轨迹上存在点C,使
交P点的轨迹于M、N两点,若P点的轨迹上存在点C,使
![]() ,求实数m的值;
,求实数m的值;
(Ⅲ)是否存在过点![]() 的直线l交P点的轨迹于点R、T,且满足
的直线l交P点的轨迹于点R、T,且满足![]() (O为原点)?若存在,求直线l的方程,若不存在,请说明理由。
(O为原点)?若存在,求直线l的方程,若不存在,请说明理由。
定长为3的线段 两端点
两端点 分别在
分别在 轴,
轴, 轴上滑动,
轴上滑动, 在线段
在线段 上,且
上,且
(1)求点 的轨迹
的轨迹 的方程.
的方程.
(2)设过 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线 交轨迹
交轨迹 与
与 两点.问:线段
两点.问:线段 上是否存在一点
上是否存在一点 ,使得以
,使得以 为邻边的平行四边形为菱形?作出判断并证明.
为邻边的平行四边形为菱形?作出判断并证明.
如图1,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则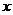 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图3,抛物线上是否存在一点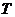 ,过点
,过点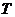 作
作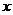 轴的垂线,垂足为
轴的垂线,垂足为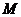 ,过点
,过点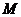 作直线
作直线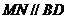 ,交线段
,交线段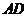 于点
于点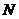 ,连接
,连接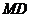 ,使
,使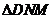 ~
~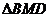 ,若存在,求出点
,若存在,求出点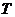 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
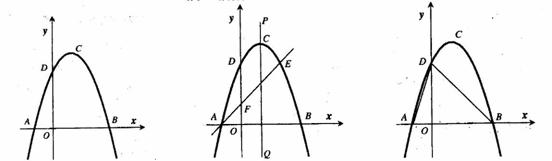 图1
图2
图3
图1
图2
图3
 。
。 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线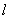 交轨迹C与A,B两点。问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。
交轨迹C与A,B两点。问:线段OF上是否存在一点D,使得以DA,DB为邻边的平行四边形为菱形?作出判断并证明。 已知点![]() 和抛物线
和抛物线![]() 的焦点
的焦点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是以点
是以点![]() 为圆心,4为半径的
为圆心,4为半径的![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 交于点
交于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,
求抛物线![]() 和曲线
和曲线![]() 的方程;
的方程;
是否存在直线![]() ,使得直线
,使得直线![]() 分别与抛物线
分别与抛物线![]() 及曲线
及曲线![]() 均只有一个公共点,若存在,求出所有这样的直线
均只有一个公共点,若存在,求出所有这样的直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
一、选择题:本题考查基本知识和基本运算,每小题5分。共60分。
CBDDD ABDAB DA
二、填空题:本题考查基本知识和基本运算,每小题4分,共16分。
(13) ---理科数学.files/image299.gif) (14) ―192 (15)
(14) ―192 (15)---理科数学.files/image301.gif) (16)
①③④
(16)
①③④
三、解答题:本大题共6小题,共74分。
(17)(本小题满分12分)
解:(Ⅰ)---理科数学.files/image303.gif) …………………………………………1分
…………………………………………1分
依题意 ---理科数学.files/image305.gif) …………………………………………2分
…………………………………………2分
又 ---理科数学.files/image307.gif)
---理科数学.files/image309.gif) …………………………………………4分
…………………………………………4分
---理科数学.files/image311.gif) …………………………………………5分
…………………………………………5分
令 x=0,得 ---理科数学.files/image313.gif) ………………………7分
………………………7分
所以, 函数---理科数学.files/image190.gif) 的解析式为
的解析式为 ---理科数学.files/image315.gif) ……………………………8分
……………………………8分
(还有其它的正确形式,如:---理科数学.files/image317.gif) 等)
等)
(Ⅱ)当---理科数学.files/image319.gif) ,
,---理科数学.files/image321.gif) 时
时---理科数学.files/image323.gif) 单增 ……10分
单增 ……10分
即---理科数学.files/image325.gif) ,
,---理科数学.files/image321.gif) …………………………………………11分
…………………………………………11分
∴---理科数学.files/image323.gif) 的增区间是
的增区间是---理科数学.files/image329.gif) ………………………………………12分
………………………………………12分
(注意其它正确形式,如:区间左右两端取开、闭,---理科数学.files/image331.gif) 等)
等)
(18)(本小题满分12分)
解:(Ⅰ)设等差数列---理科数学.files/image333.gif) 的公差为
的公差为---理科数学.files/image335.gif) ,等比数列的公比为
,等比数列的公比为---理科数学.files/image337.gif) ,
,
由题设知---理科数学.files/image339.gif) ,∴
,∴---理科数学.files/image341.gif) ,∴
,∴---理科数学.files/image343.gif)
则---理科数学.files/image345.gif) ,∴
,∴---理科数学.files/image347.gif) ………………………………3分
………………………………3分
∴---理科数学.files/image349.gif)
又∵---理科数学.files/image351.gif) ,
,
∴---理科数学.files/image353.gif) ,
,
又---理科数学.files/image355.gif) ,∴
,∴---理科数学.files/image357.gif) ,
,
∴---理科数学.files/image359.gif) ,又
,又---理科数学.files/image361.gif)
∴---理科数学.files/image363.gif) ,
,
∴---理科数学.files/image365.gif) ………………………………………………………6分
………………………………………………………6分
(Ⅱ) ---理科数学.files/image367.gif) ,……………………………………7分
,……………………………………7分
∴---理科数学.files/image369.gif)
---理科数学.files/image371.gif) ①
①
---理科数学.files/image373.gif) ②……………………………9分
②……………………………9分
①一②得---理科数学.files/image375.gif)
---理科数学.files/image377.gif)
∴---理科数学.files/image379.gif) ………………………………………………………12分
………………………………………………………12分
(19)(本小题满分12分)
解:(1)设---理科数学.files/image381.gif) ,∵几何体
,∵几何体---理科数学.files/image231.gif) 的体积为
的体积为---理科数学.files/image233.gif) ,
,
∴---理科数学.files/image384.gif) ,
………………………3分
,
………………………3分
即---理科数学.files/image386.gif) ,
,
即---理科数学.files/image388.gif) ,解得
,解得---理科数学.files/image390.gif) .
.
∴---理科数学.files/image235.gif) 的长为4.
……………………………6分
的长为4.
……………………………6分
---理科数学.files/image391.gif) (2)在线段
(2)在线段---理科数学.files/image237.gif) 上存在点
上存在点---理科数学.files/image095.gif) ,使直线
,使直线---理科数学.files/image240.gif) 与
与---理科数学.files/image242.gif) 垂直.
垂直.
以下给出两种证明方法:
方法1:过点---理科数学.files/image397.gif) 作
作---理科数学.files/image242.gif) 的垂线交
的垂线交---理科数学.files/image400.gif) 于点
于点---理科数学.files/image402.gif) ,过点
,过点---理科数学.files/image402.gif) 作
作---理科数学.files/image404.gif)
交---理科数学.files/image237.gif) 于点
于点---理科数学.files/image095.gif) .
.
∵---理科数学.files/image408.gif) ,
,---理科数学.files/image410.gif) ,
,---理科数学.files/image412.gif) ,
,
∴---理科数学.files/image414.gif) 平面
平面---理科数学.files/image416.gif) .
.
∵---理科数学.files/image418.gif) 平面
平面---理科数学.files/image416.gif) ,∴
,∴---理科数学.files/image420.gif) .
.
∵---理科数学.files/image422.gif) ,∴
,∴---理科数学.files/image414.gif) 平面
平面---理科数学.files/image424.gif) .
.
∵---理科数学.files/image426.gif) 平面
平面---理科数学.files/image424.gif) ,∴
,∴---理科数学.files/image428.gif) .
.
在矩形---理科数学.files/image430.gif) 中,∵
中,∵---理科数学.files/image432.gif) ∽
∽---理科数学.files/image434.gif) ,
,
∴---理科数学.files/image436.gif) ,即
,即---理科数学.files/image438.gif) ,∴
,∴---理科数学.files/image440.gif) .
.
∵---理科数学.files/image442.gif) ∽
∽---理科数学.files/image444.gif) ,∴
,∴---理科数学.files/image446.gif) ,即
,即---理科数学.files/image448.gif) ,∴
,∴---理科数学.files/image450.gif) .………………………9分
.………………………9分
在---理科数学.files/image452.gif) 中,∵
中,∵---理科数学.files/image454.gif) ,∴
,∴---理科数学.files/image456.gif) .
.
由余弦定理,得---理科数学.files/image458.gif)
---理科数学.files/image460.gif) .………………………11分
.………………………11分
∴在线段---理科数学.files/image237.gif) 上存在点
上存在点---理科数学.files/image095.gif) ,使直线
,使直线---理科数学.files/image240.gif) 与
与---理科数学.files/image242.gif) 垂直,且线段
垂直,且线段---理科数学.files/image240.gif) 的长为
的长为---理科数学.files/image465.gif) .
………………………12分
.
………………………12分
方法2:以点---理科数学.files/image467.gif) 为坐标原点,分别以
为坐标原点,分别以---理科数学.files/image469.gif) ,
,---理科数学.files/image471.gif) ,
,---理科数学.files/image473.gif) 所在的直线为
所在的直线为---理科数学.files/image475.gif) 轴,
轴,---理科数学.files/image477.gif) 轴,
轴,---理科数学.files/image479.gif) 轴建立如图的空间直角坐标系,由已知条件与(1)可知,
轴建立如图的空间直角坐标系,由已知条件与(1)可知,---理科数学.files/image481.gif) ,
,---理科数学.files/image483.gif) ,
,---理科数学.files/image485.gif) , ………………………7分
, ………………………7分
假设在线段---理科数学.files/image237.gif) 上存在点
上存在点---理科数学.files/image487.gif)
---理科数学.files/image489.gif) ≤
≤---理科数学.files/image475.gif) ≤2,
≤2,---理科数学.files/image492.gif) ,0≤
,0≤---理科数学.files/image479.gif) ≤
≤---理科数学.files/image495.gif)
由---理科数学.files/image505.gif) ∽
∽---理科数学.files/image507.gif) ,得
,得---理科数学.files/image509.gif) ,
,
∴---理科数学.files/image511.gif) .
.
∴---理科数学.files/image513.gif) .
.
∴---理科数学.files/image515.gif) ,
,---理科数学.files/image517.gif) .
.
∵---理科数学.files/image519.gif) ,∴
,∴---理科数学.files/image521.gif) ,
,
即---理科数学.files/image523.gif) ,∴
,∴---理科数学.files/image525.gif) . ……………………9分
. ……………………9分
此时点---理科数学.files/image095.gif) 的坐标为
的坐标为---理科数学.files/image527.gif) ,在线段
,在线段---理科数学.files/image237.gif) 上.
上.
∵---理科数学.files/image529.gif) ,∴
,∴---理科数学.files/image531.gif) .……………11分
.……………11分
∴在线段---理科数学.files/image237.gif) 上存在点
上存在点---理科数学.files/image095.gif) ,使直线
,使直线---理科数学.files/image240.gif) 与
与---理科数学.files/image242.gif) 垂直,且线段
垂直,且线段---理科数学.files/image240.gif) 的长为
的长为---理科数学.files/image465.gif) .
……………………12分
.
……………………12分
(20)(本小题满分12分)
解:(Ⅰ)---理科数学.files/image247.gif) 的所有可能值为0,1,2,3,4.…………………………1分
的所有可能值为0,1,2,3,4.…………………………1分
---理科数学.files/image533.gif) ,
,
---理科数学.files/image535.gif) ,
,
---理科数学.files/image537.gif)
---理科数学.files/image539.gif) ,
,
---理科数学.files/image541.gif) .
……………………4分
.
……………………4分
其分布列为:
---理科数学.files/image247.gif)
0
1
2
3
4
---理科数学.files/image095.gif)
---理科数学.files/image544.gif)
---理科数学.files/image546.gif)
---理科数学.files/image548.gif)
---理科数学.files/image546.gif)
---理科数学.files/image544.gif)
…………………………6分
(Ⅱ)---理科数学.files/image552.gif) ,
,
---理科数学.files/image554.gif) .
…………………………8分
.
…………………………8分
由题意可知
---理科数学.files/image556.gif) ,
…………………………10分
,
…………………………10分
---理科数学.files/image558.gif) 元. …………………………12分
元. …………………………12分
(21)(本小题满分12分)
解:(Ⅰ)因为---理科数学.files/image265.gif) ,所以有
,所以有---理科数学.files/image561.gif)
所以---理科数学.files/image563.gif) 为直角三角形;
为直角三角形;---理科数学.files/image565.gif) …………………………2分
…………………………2分
则有---理科数学.files/image567.gif)
所以,---理科数学.files/image569.gif) …………………………3分
…………………………3分
又---理科数学.files/image571.gif) ,
,---理科数学.files/image573.gif) ………………………4分
………………………4分
在---理科数学.files/image563.gif) 中有
中有---理科数学.files/image575.gif)
即---理科数学.files/image577.gif) ,解得
,解得---理科数学.files/image579.gif)
所求椭圆---理科数学.files/image269.gif) 方程为
方程为---理科数学.files/image581.gif) …………………………6分
…………………………6分
(Ⅱ)---理科数学.files/image583.gif)
---理科数学.files/image585.gif)
---理科数学.files/image587.gif)
从而将求---理科数学.files/image276.gif) 的最大值转化为求
的最大值转化为求---理科数学.files/image589.gif) 的最大值…………………………8分
的最大值…………………………8分
---理科数学.files/image095.gif) 是椭圆
是椭圆---理科数学.files/image269.gif) 上的任一点,设
上的任一点,设---理科数学.files/image591.gif) ,则有
,则有---理科数学.files/image593.gif) 即
即---理科数学.files/image595.gif)
又---理科数学.files/image597.gif) ,所以
,所以---理科数学.files/image599.gif) ………………………10分
………………………10分
而---理科数学.files/image601.gif) ,所以当
,所以当---理科数学.files/image603.gif) 时,
时,---理科数学.files/image589.gif) 取最大值
取最大值---理科数学.files/image605.gif)
故---理科数学.files/image276.gif) 的最大值为
的最大值为---理科数学.files/image607.gif) …………………………12分
…………………………12分
(22)(本小题满分14分)
(1)解法1:∵---理科数学.files/image609.gif) ,其定义域为
,其定义域为---理科数学.files/image611.gif) ,
,
∴---理科数学.files/image613.gif) .
……………………1分
.
……………………1分
∵---理科数学.files/image284.gif) 是函数
是函数---理科数学.files/image616.gif) 的极值点,∴
的极值点,∴---理科数学.files/image618.gif) ,即
,即---理科数学.files/image620.gif) .
.
∵---理科数学.files/image282.gif) ,∴
,∴---理科数学.files/image623.gif) .
.
经检验当---理科数学.files/image623.gif) 时,
时,---理科数学.files/image284.gif) 是函数
是函数---理科数学.files/image616.gif) 的极值点,
的极值点,
∴---理科数学.files/image623.gif) .
……………………5分
.
……………………5分
解法2:∵---理科数学.files/image609.gif) ,其定义域为
,其定义域为---理科数学.files/image627.gif) ,
,
∴---理科数学.files/image613.gif) .
……………………1分
.
……………………1分
令---理科数学.files/image629.gif) ,即
,即---理科数学.files/image631.gif) ,整理,得
,整理,得---理科数学.files/image633.gif) .
.
∵---理科数学.files/image635.gif) ,
,
∴---理科数学.files/image629.gif) 的两个实根
的两个实根---理科数学.files/image637.gif) (舍去),
(舍去),---理科数学.files/image639.gif) ,……………………3分
,……………………3分
当---理科数学.files/image475.gif) 变化时,
变化时,---理科数学.files/image616.gif) ,
,---理科数学.files/image643.gif) 的变化情况如下表:
的变化情况如下表:
---理科数学.files/image475.gif)
---理科数学.files/image646.gif)
---理科数学.files/image648.gif)
---理科数学.files/image650.gif)
---理科数学.files/image643.gif)
―
0
+
---理科数学.files/image616.gif)
---理科数学.files/image652.gif)
极小值
---理科数学.files/image654.gif)
依题意,---理科数学.files/image656.gif) ,即
,即---理科数学.files/image658.gif) ,……………………5分
,……………………5分
∵---理科数学.files/image282.gif) ,∴
,∴---理科数学.files/image623.gif) .
.
(2)解:对任意的---理科数学.files/image290.gif) 都有
都有---理科数学.files/image294.gif) ≥
≥---理科数学.files/image296.gif) 成立等价于对任意的
成立等价于对任意的
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com