如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

PC的中点．

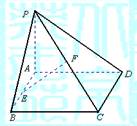
（1）求证：EF∥平面PAD；

（2）求证：EF⊥CD；

（3）若ÐPDA＝45°求EF与平面ABCD所成的角的大小．

【解析】本试题主要考查了线面平行和线线垂直的运用，以及线面角的求解的综合运用

第一问中，利用连AC，设AC中点为O，连OF、OE在△PAC中，∵ F、O分别为PC、AC的中点   ∴ FO∥PA …………①在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD∵ EF Ì 平面EFO   ∴ EF∥平面PAD．

第二问中在矩形ABCD中，∵ EO∥BC，BC⊥CD ∴ EO⊥CD  又    ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影       ∴ CD⊥EF．

第三问中，若ÐPDA＝45°，则 PA＝AD＝BC    ∵ EOBC，FOPA

∴ FO＝EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO＝45°

证：连AC，设AC中点为O，连OF、OE（1）在△PAC中，∵ F、O分别为PC、AC的中点∴ FO∥PA …………①    在△ABC中，∵ E、O分别为AB、AC的中点  ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD    

∵ EF Ì 平面EFO      ∴ EF∥平面PAD．

（2）在矩形ABCD中，∵ EO∥BC，BC⊥CD∴ EO⊥CD  又        ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC ∴ EO为EF在平面AC内的射影     ∴ CD⊥EF．

（3）若ÐPDA＝45°，则 PA＝AD＝BC         ∵ EOBC，FOPA

∴ FO＝EO 又    ∵ FO⊥平面AC   ∴ △FOE是直角三角形 ∴ ÐFEO＝45°

 

A、y=2|x|

B、y=lg(x+ x2+1 )

C、y=2x+2-x

D、y=lg 1 x+1

已知数列{a_n}为等差数列，a₁=2，且其前10项和为65，又正项数列{b_n}满足bn=

n+1

an

 (n∈N*)
（1）求数列{b_n}的通项公式；
（2）比较b₁，b₂，b₃，b₄的大小；
（3）求数列{b_n}的最大项；
（4）令c_n=lga_n，数列{c_n}是等比数列吗？说明理由．

已知a∈R，函数f（x）=x|x-a|，
（Ⅰ）当a=2时，写出函数y=f（x）的单调递增区间；
（Ⅱ）当a＞2时，求函数y=f（x）在区间[1，2]上的最小值；
（Ⅲ）设a≠0，函数f（x）在（m，n）上既有最大值又有最小值，请分别求出m、n的取值范围（用a表示）．

已知f（x）是R上的偶函数，且当x≥0时，f（x）=2^x，又a是函数g(x)=ln(x+1)-

2

x

的正零点，则f（-2），f（a），f（1.5）的大小关系是．