设F（1，0），点M在x轴上，点P在y轴上，且

（1）当点P在y轴上运动时，求点N的轨迹C的方程；

（2）设是曲线C上的点，且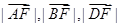成等差数列，当AD的垂直平分线与x轴交于点E（3，0）时，求点B的坐标。

【解析】本试题主要是对于圆锥曲线的综合考查。首先求解轨迹方程，利用向量作为工具表示向量的坐标，进而达到关系式的求解。第二问中利用数列的知识和直线方程求解点的坐标。

在平面直角坐标系中，曲线与坐标轴的交点都在圆上．

(1)求圆的方程；

 (2)若圆与直线交于、两点，且，求的值．

【解析】本试题主要是考查了直线与圆的位置关系的运用。

（1）曲线与轴的交点为(0,1)，

与轴的交点为(3＋2，0)，(3－2，0) 故可设的圆心为(3，t)，则有3²＋(t－1)²＝(2)²＋t²，解得t＝1.

（2）因为圆与直线交于、两点，且。联立方程组得到结论。

⊙O₁和⊙O₂的极坐标方程分别为，．

⑴把⊙O₁和⊙O₂的极坐标方程化为直角坐标方程；

⑵求经过⊙O₁，⊙O₂交点的直线的直角坐标方程．

【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用

（1）中，借助于公式，，将极坐标方程化为普通方程即可。

（2）中，根据上一问中的圆的方程，然后作差得到交线所在的直线的普通方程。

解：以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位．

(I)，，由得．所以．

即为⊙O₁的直角坐标方程．

同理为⊙O₂的直角坐标方程．

(II)解法一:由解得，

即⊙O₁，⊙O₂交于点(0,0)和(2,－2)．过交点的直线的直角坐标方程为y=－x．

解法二: 由,两式相减得－4x-4y=0,即过交点的直线的直角坐标方程为y=－x

已知椭圆＋＝1（a>b>0)上的点M (1, )到它的两焦点F₁，F₂的距离之和为4，A、B分别是它的左顶点和上顶点。
(Ⅰ)求此椭圆的方程及离心率；
(Ⅱ)平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程。

【解析】本试题主要是考查椭圆的方程和椭圆的几何性质，以及直线与椭圆的位置关系的综合运用。联立方程组，结合韦达定理求解和运算。

已知椭圆＋＝1（a>b>0)上的点M (1, )到它的两焦点F₁，F₂的距离之和为4，A、B分别是它的左顶点和上顶点。

(Ⅰ)求此椭圆的方程及离心率；

(Ⅱ)平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程。

【解析】本试题主要是考查椭圆的方程和椭圆的几何性质，以及直线与椭圆的位置关系的综合运用。联立方程组，结合韦达定理求解和运算。