
题目列表(包括答案和解析)
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)证明:当 时,
时, 恒成立;
恒成立;
(3)任取两个不相等的正数 ,且
,且 ,若存在
,若存在 使
使 成立,证明:
成立,证明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
当k 0时,
0时, >0,所以函数g(x)的增区间为(0,+
>0,所以函数g(x)的增区间为(0,+ ),无减区间;
),无减区间;
当k>0时, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增区间(k,+
<0,得0<x<k∴增区间(k,+ )减区间为(0,k)(3’)
)减区间为(0,k)(3’)
(2)设h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 当x变化时,h(x),
= lnx-1=0得x=e, 当x变化时,h(x), 的变化情况如表
的变化情况如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
设G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,当且仅当x=1时,
0,当且仅当x=1时, =0所以G(x) 为减函数, 所以G(x)
=0所以G(x) 为减函数, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,综上,当x
,综上,当x 1时, 2x-e
1时, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵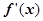 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=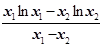 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 设H(t)=lnt+1-t(0<t<1),
(10’) 设H(t)=lnt+1-t(0<t<1),
 =
= =
=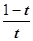 >0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
①h(x)的图象关于原点(0,0)对称;
②h(x)的图象关于y轴对称;
③h(x)的最小值为0;
④h(x)在区间(-1,0)上单调递增.
其中正确的命题是__________________.(把正确命题的序号都填上)
①h(x)的图像关于原点对称; ②h(x)为偶函数;
③h(x)的最小值为0; ④h(x)在(0,1)上为减函数.
其中正确命题的序号为_____________.(将你认为正确的命题的序号都填上)
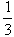 时,令h(x)=f′(x)+6x,求证:当x∈(0,+∞) 时,h(x)>2elnx(e为自然对数的底数);
时,令h(x)=f′(x)+6x,求证:当x∈(0,+∞) 时,h(x)>2elnx(e为自然对数的底数);【解析】如图:|OB|=b,|O F1|=c.∴kPQ=![]() ,kMN=﹣
,kMN=﹣![]() .
.
直线PQ为:y=![]() (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=![]() x.由
x.由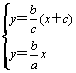 ,得:Q(
,得:Q(![]() ,
,![]() );由
);由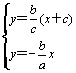 ,得:P(
,得:P(![]() ,
,![]() ).∴直线MN为:y-
).∴直线MN为:y-![]() =﹣
=﹣![]() (x-
(x-![]() ),
),
令y=0得:xM=![]() .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=![]() ,解之得:
,解之得:![]() ,即e=
,即e=![]() .
.
【答案】B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com