
题目列表(包括答案和解析)
(势能、动能及动能定理的综合)如图所示,一物体质量m=2 kg,在倾角θ=37°的斜面上的A点以初速度v0=3 m/s下滑,A点距弹簧上端挡板位置B的距离![]() =4 m.当物体到达B点时将弹簧压缩到最远点C,BC=0.2 m;然后物体又被弹回去,弹到的最高位置为D,AD=3 m.挡板及弹簧质量不计,g取10 m/s2,求:
=4 m.当物体到达B点时将弹簧压缩到最远点C,BC=0.2 m;然后物体又被弹回去,弹到的最高位置为D,AD=3 m.挡板及弹簧质量不计,g取10 m/s2,求:

(1)物体与斜面间的动摩擦因数μ;
(2)弹簧的最大弹性势能.
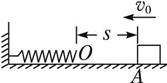
质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,如图所示.已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,则弹簧被压缩至最短时的弹性势能为( )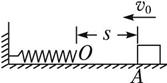
A. | B.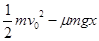 |
| C.μmgs | D.μmg(s+x) |
质量为m的物体以初速度v0沿水平面向左开始运动,起始点A与一轻弹簧O端相距s,如图所示.已知物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,则弹簧被压缩至最短时的弹性势能为( )
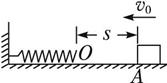
A.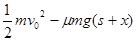 B.
B.
C.μmgs D.μmg(s+x)
A.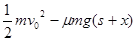 | B.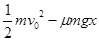 |
| C.μmgs | D.μmg(s+x) |
 轻质弹簧长为L竖直固定在地面上,质量为m的小球从离地面高度为H处由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x.设小球在运动过程中受到的阻力大小为f,则弹簧被压缩到最短时具有的弹性势能为( )
轻质弹簧长为L竖直固定在地面上,质量为m的小球从离地面高度为H处由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x.设小球在运动过程中受到的阻力大小为f,则弹簧被压缩到最短时具有的弹性势能为( )| A、(mg-f)(H-L+x) | B、mg(H-L+x)-F(H-L) | C、mgH-f(H-L) | D、mg(L-x)+f(H-L+x) |
一、选择题(每小题5分,共60分)
1.C 2.A 3.D 4.B C 5. C 6.B D
7.B 8.A 9.B 10.C 11.D 12.AD
 二、填空题和实验题(每题6分,共30分)
二、填空题和实验题(每题6分,共30分)
13.mAgcosθ; mBg - mAgsinθ 。
14.3×10―4; 1。
15.
16.a = (s2-2s1) / T2 或 a = (s3-2s2+ s1) / T2 或a = (s3-s2-s1) / 2T2;
vc = (s3-s1) / 2T 。
17.(1)如答图1;
(2)0~6.4; (3) 。
。
三、计算题(60分)
18.(10分)解:
(1)取物体运动方向为正,由平衡条件有
Fcosθ-f = 0 N = mg-Fsinθ 又f =μN
所以有 (4分)
(4分)
(2) 由牛顿第二定律有 -μmg=ma a = -μg=-0.4×
(3)据0-v02=2as, 有 m
(3分)
m
(3分)
19.(12分)解:
(1)感应电动势为 E=BLv=1.0V
感应电流为  =
=
(2)导体棒匀速运动,安培力与拉力平衡
即有F=BIL=0.1N (4分)
(3) 导体棒移动 = 0.03s
= 0.03s
根据焦耳定律, Q1 = I2R t = 0.03J (或Q1=Fs=0.03J)
根据能量守恒,
Q2= = 0.5J
= 0.5J
电阻R上产生的热量 Q = Q1+Q2 = 0.53J (4分)
20.(12分)解:
(1)能求出地球的质量M (1分)
方法一:  = mg , M =
= mg , M =
方法二:  =
=  , M =
, M = (3分)
(3分)
(写出一种方法即可)
(2)能求出飞船线速度的大小V (1分)
V = ( 或R
( 或R  ) (3分)
) (3分)
(3)不能算出飞船所需的向心力 (1分)
因飞船质量未知 (3分)
21.(12分)解:
(1)由机械能守恒定律,有
 (4分)
(4分)
(2)A、B在碰撞过程中内力远大于外力,由动量守恒,有
 (4分)
(4分)
(3)A、B克服摩擦力所做的功
由能量守恒定律,有 
解得  (4分)
(4分)
22.(14分)解:
(1)当小球离开圆弧轨道后,对其受力分析如图所示,
 由平衡条件得:F电 = qE
= mgtan
由平衡条件得:F电 = qE
= mgtan (2分)
(2分)
代入数据解得:E =3 N/C (1分)
(2)小球从进入圆弧轨道到离开圆弧轨道的过程中,由动能定理得:
F电 (2分)
(2分)
代入数据得: (1分)
(1分)
由 (2分)
(2分)
解得:B=1T (2分)
 分析小球射入圆弧轨道瞬间的受力情况如图所示,
分析小球射入圆弧轨道瞬间的受力情况如图所示,
由牛顿第二定律得: (2分)
(2分)
代入数据得: (1分)
(1分)
由牛顿第三定律得,小球对轨道的压力
 (1分)
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com