练习册

  • 练习册
  • 试题
    (Ⅲ)证明:当时.存在正数.使得不等式.成立的最小正数.并求此时的最小正数.第二部分(总分40分.加试时间30分钟)注意事项:答卷前.请考生务必将自己的学校.姓名.考试号等信息填写在答卷密封线内．解答过程应写在答题卷的相应位置上.在其它地方答题无效.[选做题]在A.B.C.D四小题中只能选做2题.每题10分.共计20分.请在答题纸指定区域内作答.解答应写出文字说明.证明过程或演算步骤. 【查看更多】

     

    题目列表(包括答案和解析)

    定义在正实数集上的函数f（x）满足下列条件：
    ①存在常数a（0＜a＜1），使得f（a）=1；②对任意实数m，当x∈R+时，有f（xm）=mf（x）．
    （1）求证：对于任意正数x，y，f（xy）=f（x）+f（y）；
    （2）证明：f（x）在正实数集上单调递减；
    （3）若不等式f（loga2（4-x）+2）-f（loga（4-x）8）≤3恒成立，求实数a的取值范围．

    查看答案和解析>>

    定义在正实数集上的函数f（x）满足下列条件：
    ①存在常数a（0＜a＜1），使得f（a）=1；②对任意实数m，当x∈R+时，有f（xm）=mf（x）．
    （1）求证：对于任意正数x，y，f（xy）=f（x）+f（y）；
    （2）证明：f（x）在正实数集上单调递减；
    （3）若不等式f（loga2（4-x）+2）-f（loga（4-x）8）≤3恒成立，求实数a的取值范围．

    查看答案和解析>>

    定义在正实数集上的函数f（x）满足下列条件：
    ①存在常数a（0＜a＜1），使得f（a）=1；②对任意实数m，当x∈R+时，有f（xm）=mf（x）．
    （1）求证：对于任意正数x，y，f（xy）=f（x）+f（y）；
    （2）证明：f（x）在正实数集上单调递减；
    （3）若不等式f（loga2（4-x）+2）-f（loga（4-x）8）≤3恒成立，求实数a的取值范围．

    查看答案和解析>>

    定义在正实数集上的函数f（x）满足下列条件：
    ①存在常数a（0＜a＜1），使得f（a）=1；②对任意实数m，当x∈R+时，有f（xm）=mf（x）．
    （1）求证：对于任意正数x，y，f（xy）=f（x）+f（y）；
    （2）证明：f（x）在正实数集上单调递减；
    （3）若不等式f（loga2（4-x）+2）-f（loga（4-x）8）≤3恒成立，求实数a的取值范围．

    查看答案和解析>>

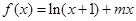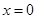    已知函数，当时，函数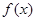取得极大值.

    （１）求实数的值；

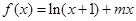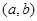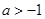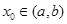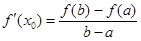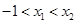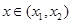    （２）已知结论：若函数在区间内导数都存在，且，则存在，使得.试用这个结论证明：若，函数，则对任意，都有；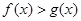

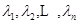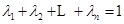    （３）已知正数，满足，求证：当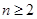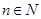，时，对任意大于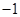，且互不相等的实数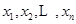，都有.

     

    查看答案和解析>>

     

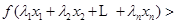
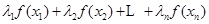    第 一 部 分

     

    一、填空题：

    1．        2．          3．1            4．16

    5．                                 6．               7．64           8．

    9．25                                 10．①④            11．        12．

    13．                          14．

    二、解答题：

    15．解：（Ⅰ）依题意：，

    即，解之得，（舍去）   …………………7分

    （Ⅱ），∴  ，，  ………………………9分

    ∴    …………………………………11分

    ．      ……………………………………………14分

    16．解：（Ⅰ）因为主视图和左视图均为矩形、所以该三棱柱为直三棱柱．

    连BC1交B1C于O，则O为BC1的中点，连DO。

    则在中，DO是中位线，

    ∴DO∥AC1．                ………………………………………………………4分

    ∵DO平面DCB1，AC1平面DCB1，

    ∴AC1∥平面CDB1．           ………………………………………………………7分

    （Ⅱ）由已知可知是直角三角形，．

    ∵  ，

    ∴  平面，平面，

    ∴   。

    ∵   ，

    ∴  平面，

    又平面，

    ∴  。

    17．解：（Ⅰ）由题意知：，

    一般地： ，…4分

    ∴  （）。……………………………………7分

    （Ⅱ）2008年诺贝尔奖发奖后基金总额为：

     ，…………………………………………10分

    2009年度诺贝尔奖各项奖金额为万美元， ………12分

    与150万美元相比少了约14万美元。     …………………………………………14分

    答：新闻 “2009年度诺贝尔奖各项奖金高达150万美元”不真，是假新闻。……15分

    18．解：（Ⅰ）圆与轴交点坐标为，

    ，，故，    …………………………………………2分

    所以，

    椭圆方程是：               …………………………………………5分

    （Ⅱ）设直线与轴的交点是，依题意，

    即,

    ,

    ,

    ,

     

    （Ⅲ）直线的方程是，…………………………………………………6分

    圆D的圆心是，半径是，……………………………………………8分

    设MN与PD相交于，则是MN的中点，且PM⊥MD，

    ……10分

    当且仅当最小时，有最小值，

    最小值即是点到直线的距离是，…………………12分

    所以的最小值是。  ……………………………15分

     

    19．解：（Ⅰ）点的坐标依次为，，…，

    ，…，           ……………………………2分

    则，…，

    若共线；则，

    即，

    即， ……………………………4分

    ，

    ，

    所以数列是等比数列。          ……………………………………………6分

    （Ⅱ）依题意，

    ，

    两式作差，则有：，   ………………………8分

    又，故，   ……………………………………………10分

    即数列是公差为的等差数列；此数列的前三项依次为

    ，

    由，可得，

    故，或，或。           ………………………………………12分

    数列的通项公式是，或，或。    ………14分

    由知，时，不合题意；

    时，不合题意；

    时，；

    所以，数列的通项公式是。  ……………………………………16分

     

    20．解：（Ⅰ）函数定义域，

    ，    ……………………………………………4分

    （Ⅱ），由（Ⅰ）

    ，，

    ，单调递增，

    所以。

    设，

    则，

    即，也就是。

    所以，存在值使得对一个，方程都有唯一解。………10分

    （Ⅲ），

    ，

    以下证明，对的数及数，不等式不成立。

    反之，由，亦即成立，

    因为，，

    但，这是不可能的。这说明是满足条件的最小正数。

    这样不等式恒成立，

    即恒成立，

    ∴  ，最小正数=4 。……………………16分

     

     第二部分（加试部分）

    21．（A）解：AD2=AE?AB，AB=4，EB=3      ……………………………………4分

    △ADE∽△ACO，                ……………………………………………8分

    CD=3                         ……………………………………………10分

    （B）解：（Ⅰ），

    所以点在作用下的点的坐标是。…………………………5分

    （Ⅱ），

    设是变换后图像上任一点，与之对应的变换前的点是，

    则，

    也就是，即，

    所以，所求曲线的方程是。……………………………………………10分

    （C）解：由已知圆的半径为，………4分

    又圆的圆心坐标为，所以圆过极点，

    所以，圆的极坐标方程是。……………………………………………10分

    （D）证明：

    ＜            ……………………………………6分

    =2－

    ＜2                              ……………………………………10分

     

     

     

    22．解：（Ⅰ）∵，∴，

    ∴切线l的方程为，即．……………………………………………4分

    （Ⅱ）令＝0，则．令＝0，则x＝1．

     ∴A＝＝＝．………………10分

    23．解：（Ⅰ）记“该生在前两次测试中至少有一次通过”的事件为事件A，则

    P(A)=

    答：该生在前两次测试中至少有一次通过的概率为。 …………………………4分

    （Ⅱ）参加测试次数的可能取值为2，3，4，

          ，

        ，

          ，    ……………………………………………7分

            故的分布列为：

    2

    3

    4

         ……………………………………………10分

    　

     

     


    同步练习册答案