
题目列表(包括答案和解析)
函数f (x)=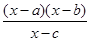 在点x=1和x=2处的极限值都为0,而在点x=-2处不连续,则x· f(x)<0的解集是( )
在点x=1和x=2处的极限值都为0,而在点x=-2处不连续,则x· f(x)<0的解集是( )
A.(-2,0)∪(1,2) B.(-2,2)
C.(-∞,-2)∪(1,2) D.(-2,0)∪(2,+∞)
如图,在三棱锥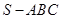 中,平面
中,平面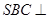 平面
平面 ,
,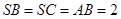 ,
,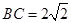 ,
,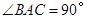 ,
,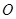 为
为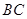 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.

【解析】第一问中利用因为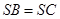 ,
, 为
为 中点,所以
中点,所以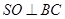
而平面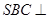 平面
平面 ,所以
,所以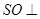 平面
平面 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以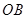 、
、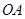 、
、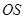 为
为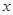 ,
,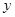 ,
,
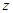 轴建立直角坐标系得
轴建立直角坐标系得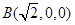 ,
,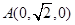 ,
,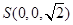 ,
,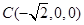 ,
,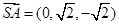 ,
,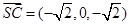 ,
,
故平面 的法向量
的法向量 而
而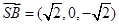 ,故点B到平面
,故点B到平面 的距离
的距离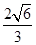
第二问中,由已知得平面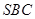 的法向量
的法向量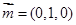 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于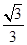
解:(Ⅰ)因为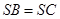 ,
,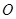 为
为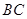 中点,所以
中点,所以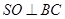
而平面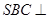 平面
平面 ,所以
,所以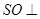 平面
平面 ,
,
再由题设条件知道可以分别以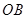 、
、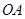 、
、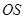 为
为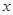 ,
,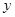 ,
,
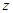 轴建立直角坐标系,得
轴建立直角坐标系,得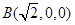 ,
,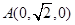 ,
,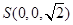 ,
,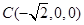 ,
,
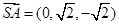 ,
,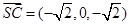 ,故平面
,故平面 的法向量
的法向量
而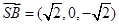 ,故点B到平面
,故点B到平面 的距离
的距离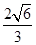
(Ⅱ)由已知得平面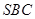 的法向量
的法向量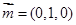 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于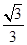
已知函数 f(x)=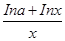 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.
【解析】本试题考查了导数在研究函数中的运用。根据函数f(x)=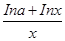 在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
在[1,+∞)上为减函数,可知导函数在给定区间恒小于等于零,f ′(x)≤0在[1,+∞)上恒成立,lna≥1-lnx在[1,+∞)上恒成立.然后利用φ(x)=1-lnx,φ(x)max=1,从而得到a≥e
f ′(x)=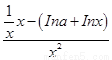 =
=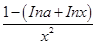 ,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
,因为 f(x)在[1,+∞)上为减函数,故 f ′(x)≤0在[1,+∞)上恒成立,即lna≥1-lnx在[1,+∞)上恒成立.设φ(x)=1-lnx,φ(x)max=1,故lna≥1,a≥e,
函数f (x)= 在点x=1和x=2处的极限值都为0,而在点x=-2处不连续,则x· f(x)<0的解集是( )
在点x=1和x=2处的极限值都为0,而在点x=-2处不连续,则x· f(x)<0的解集是( )
| A.(-2,0)∪(1,2) | B.(-2,2) |
| C.(-∞,-2)∪(1,2) | D.(-2,0)∪(2,+∞) |
3
| ||
| 2 |
| 3 |
| 2 |
| ||
| 8 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com