
题目列表(包括答案和解析)
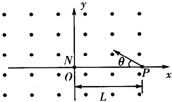 如图所示,在xOy 坐标系内有垂直纸面向外的范围足够大的匀强磁场,磁感应强度的大小为B.在t=0 时刻有两个粒子N、P分别从坐标原点O及坐标( L,0)点开始运动.N粒子带正电,电量为q,质量为m,速度大小为vn、方向为在xOy 平面内的所有可能的方向;P粒子不带电,其速度大小为vP.方向为在xOy 平面内且与x 轴的负方向的夹角为q.两粒子所受的重力不计.
如图所示,在xOy 坐标系内有垂直纸面向外的范围足够大的匀强磁场,磁感应强度的大小为B.在t=0 时刻有两个粒子N、P分别从坐标原点O及坐标( L,0)点开始运动.N粒子带正电,电量为q,质量为m,速度大小为vn、方向为在xOy 平面内的所有可能的方向;P粒子不带电,其速度大小为vP.方向为在xOy 平面内且与x 轴的负方向的夹角为q.两粒子所受的重力不计.| 3 |
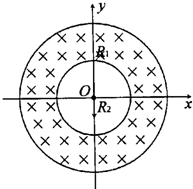 如图所示,在直角坐标系xOy决定的平面内,有两个同心圆,外侧圆半径为R1,内侧圆半径为R2,圆心为O.两圆之间的圆环内有磁感应强度为B的匀强磁场,磁场方向垂直于纸面指向纸内.在圆心O处有一质子源,沿y轴负方向发射质子流,质子流中质子的速度范围为0~v.结果有的质子从内侧圆离开磁场,有的质子从外侧圆离开磁场.已知质子带电量为e,质量为m,不考虑质子通过磁场后再进入磁场的情况.
如图所示,在直角坐标系xOy决定的平面内,有两个同心圆,外侧圆半径为R1,内侧圆半径为R2,圆心为O.两圆之间的圆环内有磁感应强度为B的匀强磁场,磁场方向垂直于纸面指向纸内.在圆心O处有一质子源,沿y轴负方向发射质子流,质子流中质子的速度范围为0~v.结果有的质子从内侧圆离开磁场,有的质子从外侧圆离开磁场.已知质子带电量为e,质量为m,不考虑质子通过磁场后再进入磁场的情况.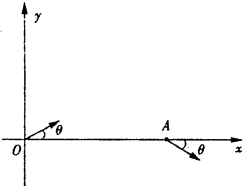 如图所示,在xOy平面内,一质量为m,电荷量为q的带电粒子(重力不计)以速度v0从坐标原点O沿与+x方向成θ角射人第一象限区,并从x轴上A的点离开第一象限区.
如图所示,在xOy平面内,一质量为m,电荷量为q的带电粒子(重力不计)以速度v0从坐标原点O沿与+x方向成θ角射人第一象限区,并从x轴上A的点离开第一象限区. 如图所示,在x轴上方平面内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一离子源,可以在平行于纸面内向x轴上方(包括x轴)沿各个方向发射速率在0到υm之间、质量为m、电量为q的负离子.不计离子的重力和离子之间的相互作用力,试分析:
如图所示,在x轴上方平面内存在方向垂直纸面向外的匀强磁场,磁感应强度大小为B.坐标原点O处有一离子源,可以在平行于纸面内向x轴上方(包括x轴)沿各个方向发射速率在0到υm之间、质量为m、电量为q的负离子.不计离子的重力和离子之间的相互作用力,试分析:| πn |
| 2qB |
| 8mmv |
| 5qB |
| πn |
| 2qB |
 如图所示,在0≤x≤a,0≤y≤2a范围内有垂直于xy平面向内的匀强磁场,在a<x≤2a,0≤y≤2a范围内有垂直于xy平面向外的匀强磁场,磁场的磁感应强度大小均为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向夹角分布在0-90°范围内,已知从(0,2a)处射出的带电粒子在磁场中运动的时间恰好为粒子在磁场中做圆周运动周期的四分之一.不计粒子重力及粒子之间相互作用,求:
如图所示,在0≤x≤a,0≤y≤2a范围内有垂直于xy平面向内的匀强磁场,在a<x≤2a,0≤y≤2a范围内有垂直于xy平面向外的匀强磁场,磁场的磁感应强度大小均为B.坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向夹角分布在0-90°范围内,已知从(0,2a)处射出的带电粒子在磁场中运动的时间恰好为粒子在磁场中做圆周运动周期的四分之一.不计粒子重力及粒子之间相互作用,求:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com