
题目列表(包括答案和解析)
(本小题满分14分)如图9所示,流程图给出了无穷整数数列![]() 满足的条件,
满足的条件,![]() ,且当k=5时,输出的S=
,且当k=5时,输出的S=![]() ;当k=10时,输出的S=
;当k=10时,输出的S=![]() 。
。![]()
(1)试求数列![]() 的通项公式
的通项公式![]() ;(2)是否存在最小的正数M使得
;(2)是否存在最小的正数M使得![]() 对一切正整数n都成立,若存在,求出M的值;若不存在,请说明理由。
对一切正整数n都成立,若存在,求出M的值;若不存在,请说明理由。 ![]()
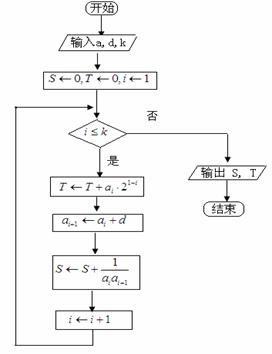
第22题图 图9
已知点 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为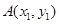 、
、 (其中
(其中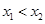 ).
).
(Ⅰ)若 ,求
,求 与
与 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是 ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,
相切,
求圆 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴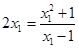 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 ,借助于函数的性质圆
,借助于函数的性质圆 面积的最小值
面积的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴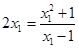 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵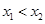 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则 的斜率
的斜率 ,
,
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即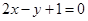 . -----------------7分
. -----------------7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即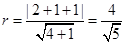 ,--------------8分
,--------------8分
故圆 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ………10分
, ………10分
∴
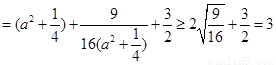 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 .
.
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
7、9、10班同学做乙题,其他班同学任选一题,若两题都做,则以较少得分计入总分.
(甲)已知f(x)=ax-ln(-x),x∈[-e,0),![]() ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若a=-1,求f(x)的极值;
(2)求证:在(1)的条件下,![]() ;
;
(3)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
(乙)定义在(0,+∞)上的函数![]() ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若函数f(x)在点x=1处连续,求a的值;
(2)若函数f(x)为(0,1)上的单调函数,求实数a的取值范围;并判断此时函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,记g(x)=lnf(x)+x2-ax. 试证明:对![]() ,当n≥2时,有
,当n≥2时,有![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com