
题目列表(包括答案和解析)
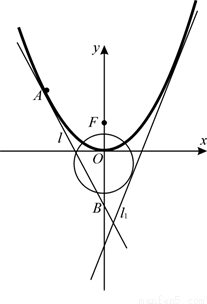
如图,已知直线 (
(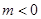 )与抛物线
)与抛物线 :
: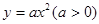 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求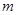 与
与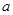 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以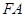 、
、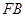 为邻边作平行四边形
为邻边作平行四边形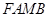 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为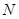 ,连接
,连接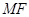 交抛物线
交抛物线 于
于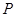 、
、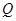 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得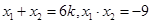 ,
…………………………… (2分)
,
…………………………… (2分)
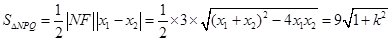 ,
,
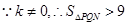 .
. △
△ 的面积
的面积 范围是
范围是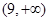
(本小题满分14分)甲、乙两间商店购进同一种商品的价格均为每件30元,销售价均为每件50元.根据前5年的有关资料统计,甲商店这种商品的年需求量![]() 服从以下分布:
服从以下分布:
|
| 10 | 20 | 30 | 40 | 50 |
|
| 0.15 | 0.20 | 0.25 | 0.30 | 0.10 |
乙商店这种商品的年需求量![]() 服从二项分布
服从二项分布![]() .
.
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理;乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推.今年甲、乙两间商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
(本小题满分14分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,若函数
,若函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“反数列”。
的“反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的反数列为
的反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)对(1)中![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若数列
,若数列![]() 的反数列为
的反数列为![]() ,
,![]() 与
与![]() 的公共项组成的数列为
的公共项组成的数列为![]() , 求数列
, 求数列![]() 前
前![]() 项和
项和![]() 。
。
(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分.)
卫生部门对某大学的4个学生食堂进行食品卫生检查(简称检查).若检查不合格,则必须整改,若整改后经复查不合格则强行关闭该食堂.设每个食堂检查是否合格是相互独立的,且每个食堂整改前检查合格的概率为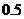 ,整改后检查合格的概率是
,整改后检查合格的概率是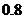 .计算(结果用小数表示,精确到
.计算(结果用小数表示,精确到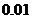 )
)
(Ⅰ)恰有一个食堂必须整改的概率;
(Ⅱ)至少关闭一个食堂的概率.
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由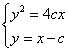 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com