
题目列表(包括答案和解析)
在正项等比数列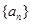 中,
中,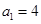 ,
, 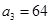 .
.
(1) 求数列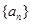 的通项公式
的通项公式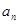 ;
;
(2) 记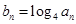 ,求数列
,求数列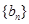 的前n项和
的前n项和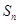 ;
;
(3) 记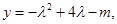 对于(2)中的
对于(2)中的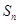 ,不等式
,不等式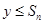 对一切正整数n及任意实数
对一切正整数n及任意实数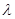 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
原命题:若p则q(p ![]() q);?
q);?
否命题:若 则 ( );?
逆命题:若 则 ( );?
逆否命题:若 则 ( ).?
(2)四种命题的关系?
?
注意:①一个命题和它的逆否命题同真假,而与它的其他三个命题的真假无此规律.?
②要严格区别命题的否定与否命题之间的差别.?
对一个命题进行否定,就要对正面叙述的词语进行否定,而否命题既否定条件又否定结论.例如,原命题“若∠A=∠B,则a=b”的否定形式为“若∠A=∠B,则a≠b”,而其否命题则为“若∠A≠∠B,则a≠b”.?
(3)反证法?
①定义: .?
②使用反证法的条件.?
(ⅰ)直接证困难较大时;?
(ⅱ)当待证命题的结论中出现“不可能”“不是”“至少”“至多”“唯一”等限制性很强的条件时.?
③一般步骤:?
(ⅰ) ;?
(ⅱ) .
某学校为了增强学生对数学史的了解,提高学生学习数学的积极性,举行了一次数学史知识竞赛,其中一道题是连线题,要求将4名数学家与他们所著的4本著作一对一边线,规定:每连对一条得5分,连错一条得-2分. 某参赛者随机用4条线把数学家与著作一对一全部连接起来.
(1)求该参赛者恰好连对一条的概率.
(2)求该参赛者得分不低于6分的概率.
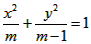 (2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。
(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D,设f (m)=||AB|-|CD| |。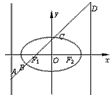
| x+1-a |
| a-x |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com