
题目列表(包括答案和解析)
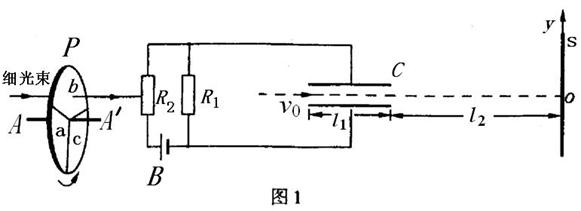
05(河北、河南、安徽、山西)16 .(20分) 图1中B为电源,电动势![]() ,内阻不计。固定电阻
,内阻不计。固定电阻![]() ,R2
,R2
为光敏电阻。C为平行板电容器,虚线到两极板距离相等,极板长![]() ,两极板的间距
,两极板的间距![]() 。S为屏,与极板垂直,到极板的距离
。S为屏,与极板垂直,到极板的距离![]() 。P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕
。P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕![]() 轴转动。当细光束通过扇形a、b、c照射光敏电阻R2时,R2的阻值分别为1000Ω、2000Ω、4500Ω。有一细电子束沿图中虚线以速度
轴转动。当细光束通过扇形a、b、c照射光敏电阻R2时,R2的阻值分别为1000Ω、2000Ω、4500Ω。有一细电子束沿图中虚线以速度![]() 连续不断地射入C。已知电子电量
连续不断地射入C。已知电子电量![]() ,电子,电子质量
,电子,电子质量![]() 。忽略细光束的宽度、电容器的充电放电时间及电子所受的重力。假设照在R2上的光强发生变化时R2阻值立即有相应的改变。
。忽略细光束的宽度、电容器的充电放电时间及电子所受的重力。假设照在R2上的光强发生变化时R2阻值立即有相应的改变。
(1)设圆盘不转动,细光束通过b照射到R2上,求电子到达屏S上时,它离O点的距离y。(计算结果保留二位有效数字)。
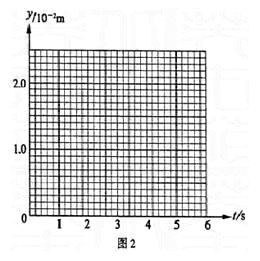
(2)设转盘按图1中箭头方向匀速转动,每3秒转一圈。取光束照在a、b分界处时t=0,试在图2给出的坐标纸上,画出电子到达屏S上时,它离O点的距离y随时间t的变化图线(0—6s间)。要求在y轴上标出图线最高点与最低点的值。(不要求写出计算过程,只按画出的图线评分。)
05(广东卷)35 ⑴如图9所示,氢原子从n>2的某一能级跃迁到n=2的能级,
 辐射出能量为2.55eV的光子。
辐射出能量为2.55eV的光子。
问最少要给基态的氢原子提供多少电子伏特的能量,才能使它
辐射上述能量的光子?请在图9中画出获得该能量后的氢原子
可能的辐射跃迁图。
05(上海卷)18 .对“落体运动快慢”、“力与物体运动关系”等问题,亚里士多德和伽利略存在着不同的观点.请完成下表:
| 亚里士多德的观点 | 伽利略的观点 | |
| 落体运动快慢 | 重的物体下落快,轻的物体下落慢 | |
| 力与物体运动关系 | 维持物体运动不需要力 |
05(上海卷)31 .(6分)部分电磁波的大致波长范围如图所
 示.若要利用缝宽与手指宽度相当的缝获得明显的衍射现象,可选用___________波段的电磁波,其原因是_______________________________________________________。
示.若要利用缝宽与手指宽度相当的缝获得明显的衍射现象,可选用___________波段的电磁波,其原因是_______________________________________________________。
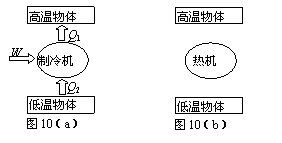
05(广东卷)67 热力学第二定律常见的表述有两种。
第一种表述:不可能使热量由低温物体传递到高温物体,而不引起其他变化;
第二种表述:不可能从单一热源吸收热量并把它全部用来做功,而不引起其他变化。
图10(a)是根据热力学第二定律的第一种表述画出的示意图:外界对制冷机做功,使热量从低温物体传递到高温物体。请你根据第二种表述完成示意图10(b)。根据你的理解,热力学第二定律的实质是_________________________。

一、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个,全部选对的得4分,选不全的得2分,有选错、多选或不选的得0分)
1.B 2.A 3.BCD 4.ABD 5.AD 6.ABD
7.C 8.BCD 9.AD 10.D 11.BD 12.CD
二、实验题(本小题共3小题,共18分)
|